Advertisements
Advertisements
Question
A current of 5.0 A exists in the circuit shown in the figure. The wire PQ has a length of 50 cm and the magnetic field in which it is immersed has a magnitude of 0.20 T. Find the magnetic force acting on the wire PQ.
Solution
Given:
Length of the wire PQ inside the magnetic field, l = 50 cm
Electric current through the wire, I = 5 A
Magnetic field, B = 0.2 T
The direction of magnetic field is perpendicular to the plane of the frame and it is going into the plane of the circuit.
As per the question,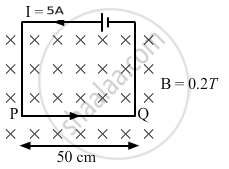
Angle between the plane of the wire and the magnetic field, θ = 90˚
Magnetic force,
`vecF = vecil xx vecB`
`therefore |vecF| = ilBsintheta`
`therefore |vecF| = ilBsin906circ`
= 5 × 50 × 10−2 × 0.2 × 1
= 0.50 N
The direction of force can be found using Fleming's left-hand rule.
Thus, the direction of magnetic force is upwards in the plane of the paper.
APPEARS IN
RELATED QUESTIONS
A small compass needle of magnetic moment ‘m’ is free to turn about an axis perpendicular to the direction of uniform magnetic field ‘B’. The moment of inertia of the needle about the axis is ‘I’. The needle is slightly disturbed from its stable position and then released. Prove that it executes simple harmonic motion. Hence deduce the expression for its time period.
A short bar magnet of magnetic moment 0.9 J/T is placed with its axis at 30° to a uniform magnetic field. It experiences a torque of 0.063 J.
(i) Calculate the magnitude of the magnetic field.
(ii) In which orientation will the bar magnet be in stable equilibrium in the magnetic field?
Can a charged particle be accelerated by a magnetic field? Can its speed be increased?
Which of the following particles will have minimum frequency of revolution when projected with the same velocity perpendicular to a magnetic field?
A particle moves in a region with a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
A wire of length l carries a current i long the x-axis. A magnetic field exists, which is given as `vecB = B_0 (veci + vecj + veck)` T. Find the magnitude of the magnetic force acting on the wire.
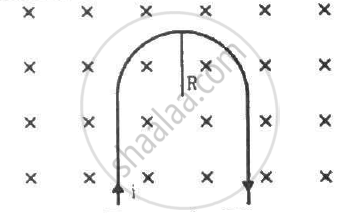
A rigid wire consists of a semi-circular portion of radius R and two straight sections (figure). The wire is partially immersed in a perpendicular magnetic field B, as shown in the figure. Find the magnetic force on the wire if it carries a current i.
Consider a straight piece of length x of a wire carrying a current i. Let P be a point on the perpendicular bisector of the piece, situated at a distance d from its middle point. Show that for d >> x, the magnetic field at P varies as 1/d2 whereas for d << x, it varies as 1/d.
A long wire carrying a current i is bent to form a place along α . Find the magnetic field B at a point on the bisector of this angle situated at a distance x from the vertex.
Figure shows a part of an electric circuit. The wires AB, CD and EF are long and have identical resistance. The separation between the neighbouring wires is 1.0 cm. The wires AE and BF have negligible resistance and the ammeter reads 30 A. Calculate the magnetic force per unit length of AB and CD.

Consider the situation shown in the figure. Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. Find the magnitude of this force when the rod makes an angle θ with the vertical.
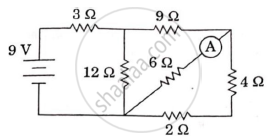
In the circuit shown in the figure, find the value of the current shown in the ammeter A.
Correct expression for force on a current carrying conductor of length dl in a magnetic field is ______.
When a magnetic compass needle is carried nearby to a straight wire carrying current, then
- the straight wire cause a noticeable deflection in the compass needle.
- the alignment of the needle is tangential to an imaginary circle with straight wire as its centre and has a plane perpendicular to the wire.
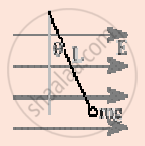
A small object with charge q and weight mg is attached to one end of a string of length ‘L’ attached to a stationary support. The system is placed in a uniform horizontal electric field ‘E’, as shown in the accompanying figure. In the presence of the field, the string makes a constant angle θ with the vertical. The sign and magnitude of q ______.
A straight conductor of length 2m moves at a speed of 20 m/s. When the conductor makes an angle of 30° with the direction of magnetic field of induction of 0.1 wbm2 then induced emf:
A conducting ring of radius 1m kept in a uniform magnetic field B of 0.01 T, rotates uniformly with an angular velocity 100 rad s−1 with its axis of rotation perpendicular to B. The maximum induced emf in it is:
