Advertisements
Advertisements
Question
A handbag contained fifty ten rupees note, thirty-five fifty rupees note and fifteen hundred rupees note. One note is drawn from a handbag. What is the probability of getting:
Fifty rupees note
Solution
Total number of notes= 50 + 35 + 15 = 100
Let E2 represent the event in which the chosen denomination is a fifty rupee note.
Number of fifty rupees note = 35
Thus, P(E2) = `"Number of fifty rupees note"/"Total number of notes"`
= `35/100`
= `7/20`
APPEARS IN
RELATED QUESTIONS
Choose the correct alternative answer for the following question and write the alphabet.
Which of the following number cannot represent a probability?
If n(A) = 5 , P(A) = `1/2` then n(S) = ?
If one die is rolled, then find the probability of the following event by completing the activity.
Event A: The number on the upper face is prime.
Activity: Let ‘S’ be the sample space.
S = {1, 2, 3, 4, 5, 6}
∴ n(S) = 6
Event A: Prime number on the upper face.
A = {`square`}
∴ n(A) = 3
P(A) = `square/(n(S))` .....[Formula]
= `square/6`
∴ P(A) = `1/square`
A card is drawn from a well shuffled pack of 52 playing cards. Find the probability of the event, the card drawn is a red card.
Activity: Let ‘S’ be the sample space.
∴ n(S) = 52
Event A: Card drawn is a red card.
∴ Total red cards = `square` hearts + 13 diamonds
∴ n(A) = `square`
∴ P(A) = `square/(n("S"))` ......[Formula]
P(A) = `26/52`
P(A) = `square`
If two coins are tossed, find the probability of event getting head on both the coins
If one die is rolled, then find the probability of event that the number on the upper face is greater than 6?
A box contains 5 strawberry chocolates, 6 coffee chocolates, and 2 peppermint chocolates. If one of the chocolates is picked from the box at random, find the probability of the following events by completing the activity.
Event A: it is coffee chocolate.
Activity: Let ‘S’ be the sample space.
∴ n(S) = 5 + 6 + 2 = 13
Event A: it is a coffee chocolate.
∴ n(A) = `square`
∴ P(A) = `square/("n"("S"))` .......[Formula]
P (A) = `square/13`
A box contains 5 strawberry chocolates, 6 coffee chocolates and 2 peppermint chocolates. If one of the chocolates is picked from the box at random, find the probability of the following events by completing the activity.
Activity : Let ‘S’ is the sample space.
∴ n(S) = 5 + 6 + 2 = 13
Event B: it is a peppermint chocolate.
∴ n(B) = `square`
∴ P(B) = `square/("n"("S"))` .......[Formula]
P(B) = `square/13`
A box contains 36 cards, bearing only one number from 1 to 36 on each. If one card is drawn at random, find the probability of an event that the card drawn bears, a prime number
A missing helicopter is reported to have crashed somewhere in the rectangular region shown in the figure. What is the probability that it crashed inside the lake shown in the figure?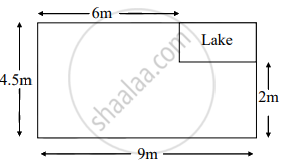
A bag contains 8 red balls and some blue balls. If one ball is drawn randomly the probability of drawing a red ball to a blue ball are in the ratio 5 : 2, determine the probability of drawing a blue ball from the bag.
In the adjoining figure, the arrow rests on any number, after the rotation of the disc. The probability that it will rest on any of the numbers on the disc is equal. Let A be any random event. To find the probability of A, fill in the boxes.

(1) S = `square`
(2) n(S) = `square`
(3) Let A be the event that arrow points at the number which is perfect cube.
A = `square`
∴ n(A) = `square`
(4) ∴ P(A) = `(n(A))/(n(S)) = square/square = square`
Using the digits 0, 2, 3, 5 the two-digit numbers are constructed without repetition of digits. Find the probability of the following events:
Condition for event A: The number formed is even.
An urn contains 12 red balls, 15 yellow balls and 18 blue balls. A ball is choosen at random, then to find the probability of choosing a blue and red coloured balls, fill in the boxes.
Total number of balls = 12 + `square` + `square` = `square`
(1) Let E be the event that the choosen ball is blue.
Number of blue balls = `square`
Thus,
P(E) = `"Number of blue balls"/"Total number of balls"`
= `square/square`
(2) Let F be the event that the choosen ball is red.
Number of red balls = `square`
Thus,
P(F) = `square/"Total number of balls"`
= `square/square`
A five digit number is formed by the digits 1, 2, 3, 4, 5 without repetition. If the probability that the number formed is divisible by 4, is P, then 5P is ______.
If six students, including two particular students A and B, stand in a row, then the probability that A and B are separated with one student in between them is ______.
