Advertisements
Advertisements
Question
A ladder 17 metre long is leaning against the wall. The base of the ladder is pulled away from the wall at a rate of 5 m/s. When the base of the ladder is 8 metres from the wall. How fast is the top of the ladder moving down the wall?
Solution
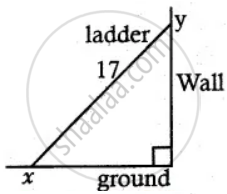
Let the height of the wall where the ladder touches are ‘y’ m.
The bottom of the ladder is at a distance of ‘x’ m from the wall.
Given x = 8, `("d"x)/"dt"` = 5
x2 + y2 = 172
Pythagoras Theorem
y2 = 172 – x2
= 289 – 64
= 225
∴ y = 15
Differentiating w.r.t. ‘t’
`2x ("d"x)/"dt" + 2y ("d"y)/"dt"` = 0 .....(÷ 2)
`x ("d"x)/"dt" + y ("d"y)/"dt"` = 0
`8(5) + 15 ("d"y)/"dt"` = 0
∴ `("d"y)/"dt" = 40/15`
= `- 8/5`
The top of the ladder is moving down the wall at the rate of `8/3` m/sec
APPEARS IN
RELATED QUESTIONS
A particle moves along a straight line in such a way that after t seconds its distance from the origin is s = 2t2 + 3t metres. Find the average velocity between t = 3 and t = 6 seconds
A particle moves along a straight line in such a way that after t seconds its distance from the origin is s = 2t2 + 3t metres. Find the instantaneous velocities at t = 3 and t = 6 seconds
A camera is accidentally knocked off an edge of a cliff 400 ft high. The camera falls a distance of s = 16t2 in t seconds. How long does the camera fall before it hits the ground?
A particle moves along a line according to the law s(t) = 2t3 – 9t2 + 12t – 4, where t ≥ 0. At what times the particle changes direction?
A particle moves along a line according to the law s(t) = 2t3 – 9t2 + 12t – 4, where t ≥ 0. Find the particle’s acceleration each time the velocity is zero
If the mass m(x) (in kilograms) of a thin rod of length x (in metres) is given by, m(x) = `sqrt(3x)` then what is the rate of change of mass with respect to the length when it is x = 3 and x = 27 metres
Find the slope of the tangent to the following curves at the respective given points.
y = x4 + 2x2 – x at x = 1
Find the point on the curve y = x2 – 5x + 4 at which the tangent is parallel to the line 3x + y = 7
Find the tangent and normal to the following curves at the given points on the curve
y = x2 – x4 at (1, 0)
Find the tangent and normal to the following curves at the given points on the curve
y = x4 + 2ex at (0, 2)
Find the tangent and normal to the following curves at the given points on the curve
y = x sin x at `(pi/2, pi/2)`
Find the angle between the rectangular hyperbola xy = 2 and the parabola x2 + 4y = 0
Choose the correct alternative:
The position of a particle moving along a horizontal line of any time t is given by s(t) = 3t2 – 2t – 8. The time at which the particle is at rest is
Choose the correct alternative:
The abscissa of the point on the curve f(x) = `sqrt(8 - 2x)` at which the slope of the tangent is – 0.25?
Choose the correct alternative:
The maximum slope of the tangent to the curve y = ex sin x, x ∈ [0, 2π] is at
