Advertisements
Advertisements
Question
A light beam of wavelength 400 nm is incident on a metal plate of work function 2.2 eV. (a) A particular electron absorbs a photon and makes two collisions before coming out of the metal. Assuming that 10% of the extra energy is lost to the metal in each collision, find the kinetic energy of this electron as it comes out of the metal. (b) Under the same assumptions, find the maximum number of collisions the electron can suffer before it becomes unable to come out of the metal.
Solution
Given :-
Wavelength of light beam, λ = 400 nm
Work function of metal plate, `phi = 2.2 "eV"`
Energy of the photon,
`E = (hc)/λ`,
Where h = Planck's constant
c = speed of light
`therefore E = 1240/400 = 3.1 "eV"`
This energy will be supplied to the electrons.
Energy lost by the electron in the first collision
= 3.1 eV × 10%
= 0.31 eV
Now, the energy of the electron after the first collision = `3.1 - 0.31 = 2.79 "eV"`
Energy lost by electron in the second collision
= 2.79 eV× 10%
= 0.279 eV
Total energy lost by the electron in two collisions
= 0.31 + 0.279 = 0.589 eV
Using Einstein's photoelectric equation, kinetic energy of the photoelectron when it comes out from the metal,
`K = E - phi - "energy lost due to collisions"`
= (3.1 − 2.2 − 0.589) eV
= 0.31 eV
(b) Similarly for the third collision, the energy lost = (2.79 - 0.279) eV × 10% = 0.2511 eV
Energy of the electron after the third collision = 2.790 - 0.2511 = 2.5389
Energy lost in the fourth collision = 2.5389 × 10%
Energy of the electron after the fourth collision = 2.5389 - 0.25389 = 2.28501
This value is very close to the work function of the metal plate. After the fifth collision, the energy of the electron becomes less than the work function of the metal.
Therefore, the electron can suffer maximum four collisions before it becomes unable to come out of the metal.
APPEARS IN
RELATED QUESTIONS
The threshold frequency for a certain metal is 3.3 × 1014 Hz. If light of frequency 8.2 × 1014 Hz is incident on the metal, predict the cutoff voltage for the photoelectric emission.
(a) A monoenergetic electron beam with electron speed of 5.20 × 106 m s−1 is subject to a magnetic field of 1.30 × 10−4 T normal to the beam velocity. What is the a radius of the circle traced by the beam, given e/m for electron equals 1.76 × 1011 C kg−1?
(b) Is the formula you employ in (a) valid for calculating the radius of the path of a 20 MeV electron beam? If not, in what way is it modified?
An electron gun with its collector at a potential of 100 V fires out electrons in a spherical bulb containing hydrogen gas at low pressure (∼10−2 mm of Hg). A magnetic field of 2.83 × 10−4 T curves the path of the electrons in a circular orbit of radius 12.0 cm. (The path can be viewed because the gas ions in the path focus the beam by attracting electrons, and emitting light by electron capture; this method is known as the ‘fine beam tube’ method. Determine e/m from the data.
Visible light has wavelengths in the range of 400 nm to 780 nm. Calculate the range of energy of the photons of visible light.
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In an experiment on photoelectric effect, light of wavelength 400 nm is incident on a cesium plate at the rate of 5.0 W. The potential of the collector plate is made sufficiently positive with respect to the emitter, so that the current reaches its saturation value. Assuming that on average, one out of every 106 photons is able to eject a photoelectron, find the photocurrent in the circuit.
A horizontal cesium plate (φ = 1.9 eV) is moved vertically downward at a constant speed v in a room full of radiation of wavelength 250 nm and above. What should be the minimum value of v so that the vertically-upward component of velocity is non-positive for each photoelectron?
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In the arrangement shown in the figure, y = 1.0 mm, d = 0.24 mm and D = 1.2 m. The work function of the material of the emitter is 2.2 eV. Find the stopping potential V needed to stop the photocurrent.
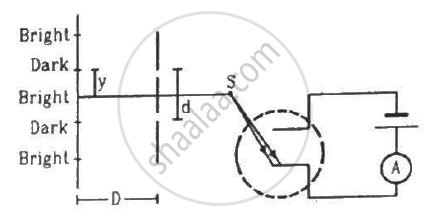
(Use h = 6.63 × 10-34J-s = 4.14 × 10-15 eV-s, c = 3 × 108 m/s and me = 9.1 × 10-31kg)
In an experiment on photoelectric effect, the emitter and the collector plates are placed at a separation of 10 cm and are connected through an ammeter without any cell. A magnetic field B exists parallel to the plates. The work function of the emitter is 2.39 eV and the light incident on it has wavelengths between 400 nm and 600 nm. Find the minimum value of B for which the current registered by the ammeter is zero. Neglect any effect of space charge.
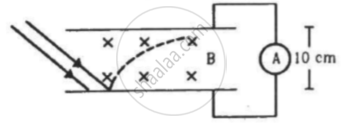
Work function of aluminium is 4.2 eV. If two photons each of energy 2.5 eV are incident on its surface, will the emission of electrons take place? Justify your answer.
Answer the following question.
Why is the wave theory of electromagnetic radiation not able to explain the photoelectric effect? How does a photon picture resolve this problem?
In the case of a photo electric effect experiment, explain the following facts, giving reasons.
The wave theory of light could not explain the existence of the threshold frequency.
In Photoelectric effect ______.
In the experimental set up for studying photoelectric effect, if keeping the frequency of the incident radiation and the accelerating potential fixed, the intensity of light is varied, then ______.
Cathode rays can be deflected by
In photoelectric effect, the photoelectric current
