Advertisements
Advertisements
Question
A plane left 30 minutes late than its scheduled time and in order to reach the destination 1500 km away in time, it had to increase its speed by 100 km/h from the usual speed. Find its usual speed.
Solution
Let the usual speed of the plane = x km/hr
Increased speed of the plane = (x + 100) km/hr
Time take to reach the destination at the usual speed, `t_1 = 1500/x` hr
Time take to reach the destination at the increased speed, `t_2 = 1500/(x + 100) hr`
Difference of both the times = t1 - t2 = 30 mins = 1/2 hr
`1500/x - 1500/(x + 100) = 1/2`
`=> 1500 (x + 100) - 1500x = (x(x + 100))/2`
`=> 1500x + 150000 - 1500x = (x(x+100))/2`
`=> 300000 = x^2 + 100x`
`=> x^2 + 100x - 300000 = 0`
`=> x^2 + 600x - 500x - 300000 = 0`
`=> (x + 600) (x - 500) = 0`
x = 500 or x = -600
As speed cannot be negative so x = 500 km/hr.
Hence, the usual speed of the plane is 500 km/hr
APPEARS IN
RELATED QUESTIONS
Classify the following polynomials as linear, quadratic, cubic and biquadratic polynomials:
`t^2+1`
In Q. No. 14, write the sign of c.
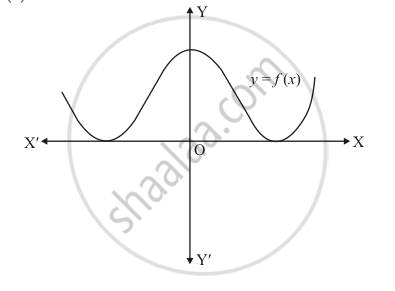
The graph of a polynomial f(x) is as shown in Fig. 2.21. Write the number of real zeros of f(x).
If α, β are the zeros of the polynomial p(x) = 4x2 + 3x + 7, then \[\frac{1}{\alpha} + \frac{1}{\beta}\] is equal to
If α and β are the zeros of the polynomial f(x) = x2 + px + q, then a polynomial having \[\frac{1}{\alpha} \text{and}\frac{1}{\beta}\] is its zero is
If the product of zeros of the polynomial f(x) ax3 − 6x2 + 11x − 6 is 4, then a =
State whether the given algebraic expression is polynomial? Justify.
10
The number of polynomials having zeroes as 4 and 7 is ______.
For the polynomial `((x^3 + 2x + 1))/5 - 7/2 x^2 - x^6`, write the coefficient of x6
Classify the following as a constant, linear, quadratic and cubic polynomials:
3
