Advertisements
Advertisements
Question
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians
Solution
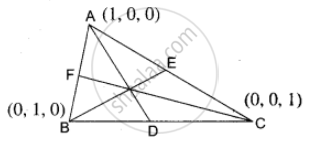
`vec"OA" = hat"i", vec"OB" = hat"j", vec"OC" = hat"k"`
D is the midpoit of BC
∴ `vec"OD" = (vec"OB" + "OC")/2`
= `(hat"j" + hat"k")/2`
E is the midpoint of AC
`vec"OE" = (hat"i" + hat"k")/2`
F is the midpoint of AB
∴ `vec"OF" = (hat"i" + hat"j")/2`
Now the medians are `vec"AD", vec"BE"` and `vec"CF"`
(i) `vec"AD" =vec"OD" - vec"OA" = (hat"j" +hat"k")/2 - hat"i"`
= `-hat"i" + hat"j"/2 + hat"k"/2`
`|vec"AD"| = sqrt(1 + 1/4 + 1/4)`
= `sqrt(1 + 1/2)`
= `sqrt(3)/sqrt(2)`
and d.c's of `vec"AD" = ((-1)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)))`
= `(- sqrt(2)/sqrt(3), sqrt(2)/(2sqrt(3)), sqrt(2)/(2sqrt(3)))`
= `(- sqrt(2)/sqrt(3), 1/(sqrt(2)sqrt(3)), 1/(sqrt(2)/sqrt(3)))`
= `(- sqrt(2)/sqrt(3), 1/sqrt(6), 1/sqrt(6))`
`["Now" sqrt(2)/sqrt(3) = sqrt(2)/sqrt(3) xx sqrt(2)/sqrt(2) = 2/sqrt(6)] = (- 2/sqrt(6), 1/sqrt(6), 1/sqrt(6))`
(ii) `vec"BE" = vec"OE" - vec"OB"`
= `(hat"i" + hat"k")/2 -hat"j"`
= `hat"i"/2 - hat"j" + hat"k"/2`
`|vec"BE"| = sqrt(1/4 + 1 + 1/4)`
= `sqrt(3)/sqrt(2)`
d.c's of `vec"BE" = ((1/2)/(sqrt(3)/sqrt(2)), (-1)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2))) = (1/sqrt(6), (-2)/sqrt(6), 1/sqrt(6))`
(iii) `vec"CE" = vec"OF" - vec"OC"`
= `(hat"i" + hat"j")/2 - hat"k"`
= `hat"i"/2 + hat"j"/2 - hat"k"`
`|vec"CF"| = sqrt(1/4 + 1/4 + 1)`
= `sqrt(3)/sqrt(2)`
d.c's of `vec"CF" = ((1/2)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)), (-1)/(sqrt(3)/sqrt(2)))`
= `(1/sqrt(6), 1/sqrt(6), (-2)/sqrt(6))`
APPEARS IN
RELATED QUESTIONS
If the lines `(x-1)/(-3) = (y -2)/(2k) = (z-3)/2 and (x-1)/(3k) = (y-1)/1 = (z -6)/(-5)` are perpendicular, find the value of k.
Find the direction cosines of the line passing through two points (−2, 4, −5) and (1, 2, 3) .
Show that the points (2, 3, 4), (−1, −2, 1), (5, 8, 7) are collinear.
What are the direction cosines of Z-axis?
Write the coordinates of the projection of point P (x, y, z) on XOZ-plane.
Write direction cosines of a line parallel to z-axis.
If the x-coordinate of a point P on the join of Q (2, 2, 1) and R (5, 1, −2) is 4, then its z-coordinate is
Ratio in which the xy-plane divides the join of (1, 2, 3) and (4, 2, 1) is
Find the direction cosines and direction ratios for the following vector
`hat"j"`
Find the direction cosines and direction ratios for the following vector
`5hat"i" - 3hat"j" - 48hat"k"`
Find the direction cosines and direction ratios for the following vector
`3hat"i" - 3hat"k" + 4hat"j"`
Choose the correct alternative:
The unit vector parallel to the resultant of the vectors `hat"i" + hat"j" - hat"k"` and `hat"i" - 2hat"j" + hat"k"` is
If α, β, γ are the angles that a line makes with the positive direction of x, y, z axis, respectively, then the direction cosines of the line are ______.
Find the equations of the two lines through the origin which intersect the line `(x - 3)/2 = (y - 3)/1 = z/1` at angles of `pi/3` each.
If the directions cosines of a line are k,k,k, then ______.
The direction cosines of vector `(2hat"i" + 2hat"j" - hat"k")` are ______.
If a line makes angles 90°, 135°, 45° with x, y and z-axis respectively then which of the following will be its direction cosine.
A line in the 3-dimensional space makes an angle θ `(0 < θ ≤ π/2)` with both the x and y axes. Then the set of all values of θ is the interval ______.
If the equation of a line is x = ay + b, z = cy + d, then find the direction ratios of the line and a point on the line.
