Advertisements
Advertisements
प्रश्न
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians
उत्तर
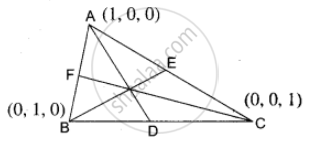
`vec"OA" = hat"i", vec"OB" = hat"j", vec"OC" = hat"k"`
D is the midpoit of BC
∴ `vec"OD" = (vec"OB" + "OC")/2`
= `(hat"j" + hat"k")/2`
E is the midpoint of AC
`vec"OE" = (hat"i" + hat"k")/2`
F is the midpoint of AB
∴ `vec"OF" = (hat"i" + hat"j")/2`
Now the medians are `vec"AD", vec"BE"` and `vec"CF"`
(i) `vec"AD" =vec"OD" - vec"OA" = (hat"j" +hat"k")/2 - hat"i"`
= `-hat"i" + hat"j"/2 + hat"k"/2`
`|vec"AD"| = sqrt(1 + 1/4 + 1/4)`
= `sqrt(1 + 1/2)`
= `sqrt(3)/sqrt(2)`
and d.c's of `vec"AD" = ((-1)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)))`
= `(- sqrt(2)/sqrt(3), sqrt(2)/(2sqrt(3)), sqrt(2)/(2sqrt(3)))`
= `(- sqrt(2)/sqrt(3), 1/(sqrt(2)sqrt(3)), 1/(sqrt(2)/sqrt(3)))`
= `(- sqrt(2)/sqrt(3), 1/sqrt(6), 1/sqrt(6))`
`["Now" sqrt(2)/sqrt(3) = sqrt(2)/sqrt(3) xx sqrt(2)/sqrt(2) = 2/sqrt(6)] = (- 2/sqrt(6), 1/sqrt(6), 1/sqrt(6))`
(ii) `vec"BE" = vec"OE" - vec"OB"`
= `(hat"i" + hat"k")/2 -hat"j"`
= `hat"i"/2 - hat"j" + hat"k"/2`
`|vec"BE"| = sqrt(1/4 + 1 + 1/4)`
= `sqrt(3)/sqrt(2)`
d.c's of `vec"BE" = ((1/2)/(sqrt(3)/sqrt(2)), (-1)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2))) = (1/sqrt(6), (-2)/sqrt(6), 1/sqrt(6))`
(iii) `vec"CE" = vec"OF" - vec"OC"`
= `(hat"i" + hat"j")/2 - hat"k"`
= `hat"i"/2 + hat"j"/2 - hat"k"`
`|vec"CF"| = sqrt(1/4 + 1/4 + 1)`
= `sqrt(3)/sqrt(2)`
d.c's of `vec"CF" = ((1/2)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)), (-1)/(sqrt(3)/sqrt(2)))`
= `(1/sqrt(6), 1/sqrt(6), (-2)/sqrt(6))`
APPEARS IN
संबंधित प्रश्न
Find the direction cosines of the line perpendicular to the lines whose direction ratios are -2, 1,-1 and -3, - 4, 1
Find the direction cosines of a line which makes equal angles with the coordinate axes.
Show that the line through points (4, 7, 8) and (2, 3, 4) is parallel to the line through the points (−1, −2, 1) and (1, 2, 5).
Write the distance of the point (3, −5, 12) from X-axis?
Write the ratio in which the line segment joining (a, b, c) and (−a, −c, −b) is divided by the xy-plane.
Ratio in which the xy-plane divides the join of (1, 2, 3) and (4, 2, 1) is
If P (3, 2, −4), Q (5, 4, −6) and R (9, 8, −10) are collinear, then R divides PQ in the ratio
Verify whether the following ratios are direction cosines of some vector or not
`1/sqrt(2), 1/2, 1/2`
Verify whether the following ratios are direction cosines of some vector or not
`4/3, 0, 3/4`
Find the direction cosines of a vector whose direction ratios are
`1/sqrt(2), 1/2, 1/2`
Find the direction cosines of the line passing through the points P(2, 3, 5) and Q(–1, 2, 4).
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
If a variable line in two adjacent positions has direction cosines l, m, n and l + δl, m + δm, n + δn, show that the small angle δθ between the two positions is given by δθ2 = δl2 + δm2 + δn2
Find the direction cosine of a line which makes equal angle with coordinate axes.
If a line has the direction ratio – 18, 12, – 4, then what are its direction cosine.
A line passes through the points (6, –7, –1) and (2, –3, 1). The direction cosines of the line so directed that the angle made by it with positive direction of x-axis is acute, are ______.
If two straight lines whose direction cosines are given by the relations l + m – n = 0, 3l2 + m2 + cnl = 0 are parallel, then the positive value of c is ______.
Equation of line passing through origin and making 30°, 60° and 90° with x, y, z axes respectively, is ______.
Find the coordinates of the foot of the perpendicular drawn from point (5, 7, 3) to the line `(x - 15)/3 = (y - 29)/8 = (z - 5)/-5`.
