Advertisements
Advertisements
प्रश्न
A triangle is formed by joining the points (1, 0, 0), (0, 1, 0) and (0, 0, 1). Find the direction cosines of the medians
उत्तर
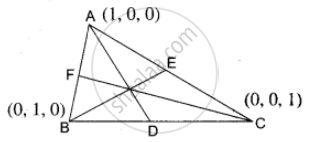
`vec"OA" = hat"i", vec"OB" = hat"j", vec"OC" = hat"k"`
D is the midpoit of BC
∴ `vec"OD" = (vec"OB" + "OC")/2`
= `(hat"j" + hat"k")/2`
E is the midpoint of AC
`vec"OE" = (hat"i" + hat"k")/2`
F is the midpoint of AB
∴ `vec"OF" = (hat"i" + hat"j")/2`
Now the medians are `vec"AD", vec"BE"` and `vec"CF"`
(i) `vec"AD" =vec"OD" - vec"OA" = (hat"j" +hat"k")/2 - hat"i"`
= `-hat"i" + hat"j"/2 + hat"k"/2`
`|vec"AD"| = sqrt(1 + 1/4 + 1/4)`
= `sqrt(1 + 1/2)`
= `sqrt(3)/sqrt(2)`
and d.c's of `vec"AD" = ((-1)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)))`
= `(- sqrt(2)/sqrt(3), sqrt(2)/(2sqrt(3)), sqrt(2)/(2sqrt(3)))`
= `(- sqrt(2)/sqrt(3), 1/(sqrt(2)sqrt(3)), 1/(sqrt(2)/sqrt(3)))`
= `(- sqrt(2)/sqrt(3), 1/sqrt(6), 1/sqrt(6))`
`["Now" sqrt(2)/sqrt(3) = sqrt(2)/sqrt(3) xx sqrt(2)/sqrt(2) = 2/sqrt(6)] = (- 2/sqrt(6), 1/sqrt(6), 1/sqrt(6))`
(ii) `vec"BE" = vec"OE" - vec"OB"`
= `(hat"i" + hat"k")/2 -hat"j"`
= `hat"i"/2 - hat"j" + hat"k"/2`
`|vec"BE"| = sqrt(1/4 + 1 + 1/4)`
= `sqrt(3)/sqrt(2)`
d.c's of `vec"BE" = ((1/2)/(sqrt(3)/sqrt(2)), (-1)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2))) = (1/sqrt(6), (-2)/sqrt(6), 1/sqrt(6))`
(iii) `vec"CE" = vec"OF" - vec"OC"`
= `(hat"i" + hat"j")/2 - hat"k"`
= `hat"i"/2 + hat"j"/2 - hat"k"`
`|vec"CF"| = sqrt(1/4 + 1/4 + 1)`
= `sqrt(3)/sqrt(2)`
d.c's of `vec"CF" = ((1/2)/(sqrt(3)/sqrt(2)), (1/2)/(sqrt(3)/sqrt(2)), (-1)/(sqrt(3)/sqrt(2)))`
= `(1/sqrt(6), 1/sqrt(6), (-2)/sqrt(6))`
APPEARS IN
संबंधित प्रश्न
Find the direction cosines of the line perpendicular to the lines whose direction ratios are -2, 1,-1 and -3, - 4, 1
Which of the following represents direction cosines of the line :
(a)`0,1/sqrt2,1/2`
(b)`0,-sqrt3/2,1/sqrt2`
(c)`0,sqrt3/2,1/2`
(d)`1/2,1/2,1/2`
Write the direction ratios of the following line :
`x = −3, (y−4)/3 =( 2 −z)/1`
Find the direction cosines of a line which makes equal angles with the coordinate axes.
If a line has the direction ratios −18, 12, −4, then what are its direction cosines?
If a line has direction ratios 2, −1, −2, determine its direction cosines.
Find the angle between the lines whose direction cosines are given by the equations
(i) l + m + n = 0 and l2 + m2 − n2 = 0
Find the angle between the lines whose direction cosines are given by the equations
2l − m + 2n = 0 and mn + nl + lm = 0
Find the angle between the lines whose direction cosines are given by the equations
2l + 2m − n = 0, mn + ln + lm = 0
What are the direction cosines of Z-axis?
If a line makes angles α, β and γ with the coordinate axes, find the value of cos2α + cos2β + cos2γ.
Write the angle between the lines whose direction ratios are proportional to 1, −2, 1 and 4, 3, 2.
If the x-coordinate of a point P on the join of Q (2, 2, 1) and R (5, 1, −2) is 4, then its z-coordinate is
Ratio in which the xy-plane divides the join of (1, 2, 3) and (4, 2, 1) is
Find the equation of the lines passing through the point (2, 1, 3) and perpendicular to the lines
If a line makes angles 90°, 135°, 45° with the x, y and z axes respectively, find its direction cosines.
Find the direction cosines of a vector whose direction ratios are
1, 2, 3
If `vec"a" = 2hat"i" + 3hat"j" - 4hat"k", vec"b" = 3hat"i" - 4hat"j" - 5hat"k"`, and `vec"c" = -3hat"i" + 2hat"j" + 3hat"k"`, find the magnitude and direction cosines of `3vec"a"- 2vec"b"+ 5vec"c"`
If a line makes an angle of 30°, 60°, 90° with the positive direction of x, y, z-axes, respectively, then find its direction cosines.
