Advertisements
Advertisements
Question
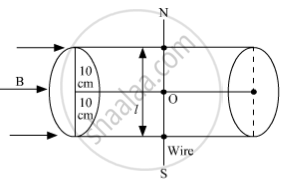
A uniform magnetic field of 1.5 T exists in a cylindrical region of radius 10.0 cm, its direction parallel to the axis along east to west. A wire carrying current of 7.0 A in the north to south direction passes through this region. What is the magnitude and direction of the force on the wire if,
(a) the wire intersects the axis,
(b) the wire is turned from N-S to northeast-northwest direction,
(c) the wire in the N-S direction is lowered from the axis by a distance of 6.0 cm?
Solution
Magnetic field strength, B = 1.5 T
Radius of the cylindrical region, r = 10 cm = 0.1 m
Current in the wire passing through the cylindrical region, I = 7 A
(a) If the wire intersects the axis, then the length of the wire is the diameter of the cylindrical region.
Thus, l = 2r = 0.2 m
Angle between magnetic field and current, θ = 90°
Magnetic force acting on the wire is given by the relation,
F = BIl sin θ
= 1.5 × 7 × 0.2 × sin 90°
= 2.1 N
Hence, a force of 2.1 N acts on the wire in a vertically downward direction.
(b) New length of the wire after turning it to the Northeast-Northwest direction can be given as:
I1 = `"l"/sin θ`
Angle between magnetic field and current, θ = 45°
Force on the wire,
F = BIl1 sin θ
= BIl
= 1.5 × 7 × 0.2
= 2.1 N
Hence, a force of 2.1 N acts vertically downward on the wire. This is independent of angleθbecause l sinθ is fixed.
(c) The wire is lowered from the axis by distance, d = 6.0 cm
Suppose wire is passing perpendicularly to the axis of cylindrical magnetic field then lowering 6 cm means displacing the wire 6 cm from its initial position towards to end of the cross-sectional area.
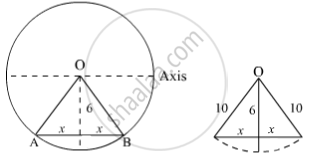
x = `sqrt(10^2 - 6^2)`
= 8 cm
Thus the length of wire in a magnetic field will be 16 cm as AB = L = 2x = 16 cm
Now the force,
F = iLB sin 90° as the wire will be perpendicular to the magnetic field.
F = 7 × 0.16 × 1.5 = 1.68 N
The direction will be given by the right-hand curl rule or screw rule i.e. vertically downwards.
APPEARS IN
RELATED QUESTIONS
Write the expression for Lorentz magnetic force on a particle of charge ‘q’ moving with velocity `vecv` in a magnetic field`vecB`. Show that no work is done by this force on the charged particle.
A beam consisting of protons and electrons moving at the same speed goes through a thin region in which there is a magnetic field perpendicular to the beam. The protons and the electrons
If a charged particle at rest experiences no electromagnetic force,
(a) the electric field must be zero
(b) the magnetic field must be zero
(c) the electric field may or may not be zero
(d) the magnetic field may or may not be zero
An experimenter's diary reads as follows: "A charged particle is projected in a magnetic field of `(7.0 vec i - 3.0 vecj)xx 10^-3 `T. The acceleration of the particle is found to be `(x veci + 7.0 vecj )` The number to the left of i in the last expression was not readable. What can this number be?
A 10 g bullet with a charge of 4.00 μC is fired at a speed of 270 m s−1 in a horizontal direction. A vertical magnetic field of 500 µT exists in the space. Find the deflection of the bullet due to the magnetic field as it travels through 100 m. Make appropriate approximations.
Using the formula \[\vec{F} = q \vec{v} \times \vec{B} \text{ and } B = \frac{\mu_0 i}{2\pi r}\]show that the SI units of the magnetic field B and the permeability constant µ0 may be written as N mA−1 and NA−2 respectively.
An electron of kinetic energy 100 eV circulates in a path of radius 10 cm in a magnetic field. Find the magnetic field and the number of revolutions per second made by the electron.
Protons with kinetic energy K emerge from an accelerator as a narrow beam. The beam is bent by a perpendicular magnetic field, so that it just misses a plane target kept at a distance l in front of the accelerator. Find the magnetic field.
A narrow beam of singly-charged carbon ions, moving at a constant velocity of 6.0 × 104m s−1, is sent perpendicularly in a rectangular region of uniform magnetic field B = 0.5 T (figure). It is found that two beams emerge from the field in the backward direction, the separations from the incident beam being 3.0 cm and 3.5 cm. Identify the isotopes present in the ion beam. Take the mass of an ion = A(1.6 × 10−27) kg, where A is the mass number.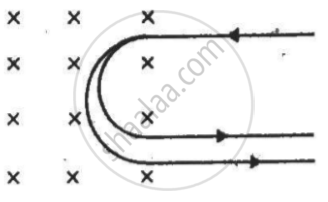
A uniform magnetic field of magnitude 0.20 T exists in space from east to west. With what speed should a particle of mass 0.010 g and with charge 1.0 × 10−5 C be projected from south to north so that it moves with uniform velocity?
