Advertisements
Advertisements
Question
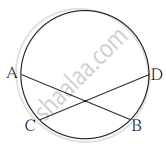
आकृति में, जीवा AB ≅ जीवा CD, तो सिद्ध कीजिए - चाप AC ≅ चाप BD
Solution
जीवा AB ≅ जीवा CD ...........(दत्त)
∴ चाप ACB ≅ चाप CBD ..........(सर्वांगसम जिवाओं संगत चाप)
∴ m(चाप ACB) = m(चाप CBD) .........(1)
m(चाप ACB) = m(चाप AC) + m(चाप CB) ..........(2)
m(चाप CBD) = m(चाप CB) + m(चाप BD) ..........(3)
(1), (2) और (3) से,
m(चाप AC) + m(चाप CB) = m(चाप CB) + m(चाप BD)
∴ m(चाप AC) = m(चाप BD)
∴ चाप AC ≅ चाप BD
APPEARS IN
RELATED QUESTIONS
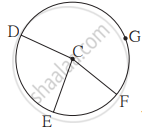
आकृति में, C केंद्रवाले वृत्त पर G, D, E और F बिंदु हैं। ∠ECF का माप 70° और चाप DGF का माप 200° हो, तो चाप DE और चाप DEF के माप ज्ञात कीजिए।
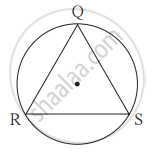
आकृति में ΔQRS समबाहु त्रिभुज है। तो सिद्ध कीजिए -
(1) चाप RS ≅ चाप QS ≅ चाप QR
(2) चाप QRS का माप 240° है।
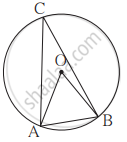
आकृति में, O केंद्र वालेवृत्त की जीवा AB की लंबाई वृत्त की त्रिज्या के बराबर है। तो (1) ∠AOB (2) ∠ACB (3) चाप AB और (4) चाप ACB का माप ज्ञात कीजिए।
आकृति में जीवा AC और जीवा DE बिंदु B पर प्रतिच्छेदित करती हैं। यदि ∠ABE = 108° और m(चाप AE) = 95° तो m(चाप DC) ज्ञात कीजिए।

दिए गए प्रत्येक उप प्रश्न के लिए चार वैकल्पिक उत्तर दिए हैं। उनमें से उचित विकल्प चुनकर लिखिए।
किसी वृत्त पर बिंदु A, B, C इस प्रकार है, कि m(चाप) AB = m(चाप BC) = 120° और दोनों चापों का कोई भी बिंदु सामान्य नहीं है। तो ΔABC किस प्रकार का त्रिभुज है?
संलग्न आकृति में, O केंद्रवाले वृत्त में रेख PQ तथा रेख RS सर्वांगसम जीवा हैं। यदि ∠POR = 70° तथा m(चाप RS) = 80°, तो -
(1) m(चाप PR) कितना?
(2) m(चाप QS) कितना?
(3) m(चाप QSR) कितना?