Advertisements
Advertisements
Question
दिए गए प्रत्येक उप प्रश्न के लिए चार वैकल्पिक उत्तर दिए हैं। उनमें से उचित विकल्प चुनकर लिखिए।
किसी वृत्त पर बिंदु A, B, C इस प्रकार है, कि m(चाप) AB = m(चाप BC) = 120° और दोनों चापों का कोई भी बिंदु सामान्य नहीं है। तो ΔABC किस प्रकार का त्रिभुज है?
Options
समबाहु त्रिभुज
विषमबाहु त्रिभुज
समकोण त्रिभुज
समद्विबाहु त्रिभुज
Solution
समबाहु त्रिभुज
APPEARS IN
RELATED QUESTIONS
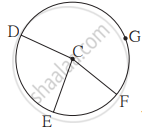
आकृति में, C केंद्रवाले वृत्त पर G, D, E और F बिंदु हैं। ∠ECF का माप 70° और चाप DGF का माप 200° हो, तो चाप DE और चाप DEF के माप ज्ञात कीजिए।
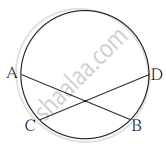
आकृति में, जीवा AB ≅ जीवा CD, तो सिद्ध कीजिए - चाप AC ≅ चाप BD
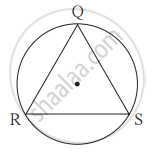
आकृति में ΔQRS समबाहु त्रिभुज है। तो सिद्ध कीजिए -
(1) चाप RS ≅ चाप QS ≅ चाप QR
(2) चाप QRS का माप 240° है।
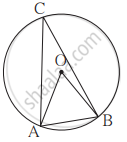
आकृति में, O केंद्र वालेवृत्त की जीवा AB की लंबाई वृत्त की त्रिज्या के बराबर है। तो (1) ∠AOB (2) ∠ACB (3) चाप AB और (4) चाप ACB का माप ज्ञात कीजिए।
आकृति में जीवा AC और जीवा DE बिंदु B पर प्रतिच्छेदित करती हैं। यदि ∠ABE = 108° और m(चाप AE) = 95° तो m(चाप DC) ज्ञात कीजिए।

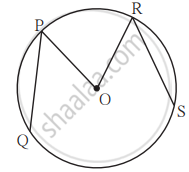
संलग्न आकृति में, O केंद्रवाले वृत्त में रेख PQ तथा रेख RS सर्वांगसम जीवा हैं। यदि ∠POR = 70° तथा m(चाप RS) = 80°, तो -
(1) m(चाप PR) कितना?
(2) m(चाप QS) कितना?
(3) m(चाप QSR) कितना?