Advertisements
Advertisements
Question
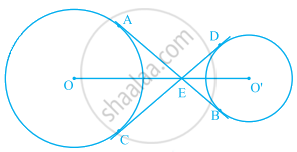
आकृति में, केंद्रों O और O' वाले दो वृत्तों की उभयनिष्ठ स्पर्श रेखाएँ AB और CD परस्पर E पर प्रतिच्छेद करती हैं। सिद्ध कीजिए कि बिंदु O, E, O' संरेखी हैं।
Solution
AO, OC और O'D, O'B को जोड़ें।
अब, ∆EO'D और ∆EO'B में,
O’D = O’B
O’E = O’E
ED = EB ...[बाहरी बिंदु से वृत्त पर खींची गई स्पर्शरेखाएं लंबाई में बराबर होती हैं।]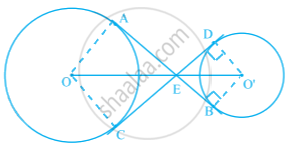
∴ EO’D ≅ ∆ EO’B ...[SSS सर्वांगसमता मानदंड द्वारा]
⇒ ∠O’ED = ∠O’EB ...(i)
अर्थात्, O'E, ∠DEB का कोण समद्विभाजक है।
इसी प्रकार, OE ∠AEC का कोण समद्विभाजक है।
अब, चतुर्भुज DEBO' में।
∠O’DE = ∠O’BE = 90° ...[CED वृत्त की एक स्पर्श रेखा है और O'D त्रिज्या है, अर्थात, O'D ⊥ CED]
⇒ ∠O’DE + ∠O’BE = 180°
∴ ∠DEB + ∠DO’B = 180° ...(ii) [∵ DEBO' चक्रीय चतुर्भुज है।]
चूँकि, AB एक सीधी रेखा है।
∴ ∠AED + ∠DEB = 180°
⇒ ∠AED + 180° – ∠DO’B = 180° ...[From (ii)]
⇒ ∠AED = ∠DO’B ...(iii)
इसी प्रकार, ∠AED = ∠AOC ...(iv)
पुनः समीकरण (ii) से,
∠DEB = 180° – ∠DO’B
दोनों ओर 2 से भाग देने पर, हमें प्राप्त होता है।
`1/2 ∠"DEB" = 90^circ - 1/2 ∠"DO'B"`
⇒ ∠DE'O = 90° `-1/2` ∠DO'B ...(v) [∵ O'E, ∠DEB का कोण समद्विभाजक है अर्थात `1/2` ∠DEB = ∠DEO']
इसी प्रकार, ∠AEC = 180° – ∠AOC
दोनों ओर 2 से भाग देने पर, हमें प्राप्त होता है।
`1/2 ∠"AEC" = 90^circ - 1/2 ∠"AOC"`
⇒ `∠"AEO" = 90^circ - 1/2 ∠"AOC"` ...(vi) [∵ OE, ∠AEC का कोण समद्विभाजक है, अर्थात, `1/2 ∠"AEC" = ∠"AEO" `]
अब, ∠AED + ∠DEO' + ∠AEO = ∠AED + `(90^circ - 1/2 ∠"DO'B") + (90^circ - 1/2 ∠"AOC")`
= `∠"AED" + 180^circ - 1/2 (∠"DO'B" + ∠"AOC")`
= `∠"AED" + 180^circ - 1/2 (∠"AED" + ∠"AED")` ...[समीकरण (iii) और (iv) से]
= `∠"AED" + 180^circ - 1/2 (2 xx ∠"AED")`
= ∠AED + 180° – ∠AED = 180°
∴ ∠AED + ∠DEO' + ∠AEO = 180°
तो, OEO' सीधी रेखा है।
अतः, O, E और O' संरेख हैं।
APPEARS IN
RELATED QUESTIONS
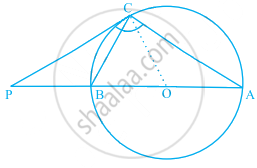
आकृति में, यदि PQR केंद्र O वाले वृत्त की बिंदु Q पर स्पर्श रेखा है, AB रेखा PR के समांतर एक जीवा है तथा ∠BQR = 70° है, तो ∠AQB बराबर ______ है।
दो संकेंद्रीय वृत्तों में से बाहरी वृत्त की त्रिज्या 5 cm है तथा इसकी 8 cm लंबी जीवा AC आंतरिक वृत्त की स्पर्श रेखा है। आंतरिक वृत्त की त्रिज्या ज्ञात कीजिए।
सिद्ध कीजिए कि किसी वृत्त की एक जीवा के सिरों पर खींची गई स्पर्श रेखाएँ उस जीवा से बराबर कोण बनाती हैं।
यदि केंद्र O वाले वृत्त की AB एक जीवा है, AOC एक व्यास है तथा AT बिंदु A पर खींची गई स्पर्श रेखा है, जैसा कि आकृति में दर्शाया गया है। सिद्ध कीजिए कि ∠BAT = ∠ACB है।
केंद्रों O और O' वाले तथा क्रमशः त्रिज्याओं 3 cm और 4 cm वाले दो वृत्त परस्पर बिंदुओं P और Q पर इस प्रकार प्रतिच्छेद करते हैं। कि OP और O' P दोनों वृत्तों की स्पर्श रेखाएँ हैं। उभयनिष्ठ जीवा PQ की लंबाई ज्ञात कीजिए।
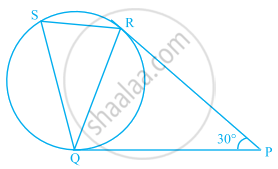
आकृति में, एक वृत्त पर दो स्पर्श रेखाएँ PQ और PR इस प्रकार खींची गई हैं कि ∠RPQ = 30° है। एक जीवा RS स्पर्श रेखा PQ के समांतर खींची जाती है। ∠RQS ज्ञात कीजिए।
[संकेत: Q से होकर जाती हुई QP पर एक लंब रेखा खींचिए।]
केंद्र O वाले किसी वृत्त का AB एक व्यास है और AC एक जीवा इस प्रकार है कि ∠BAC = 30° है। C पर वृत्त की स्पर्श रेखा बढ़ाई गई AB को बिंदु D पर प्रतिच्छेद करती है। सिद्ध कीजिए कि BC = BD है।
सिद्ध कीजिए कि किसी वृत्त के एक चाप के मध्य-बिंदु पर वृत्त की स्पर्श रेखा उस चाप के सिरों को मिलाने वाली जीवा के समांतर होती है।
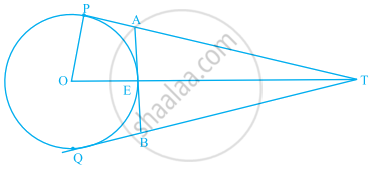
आकृति में, O त्रिज्या 5 cm वाले वृत्त का केंद्र है, T एक बिंदु इस प्रकार है कि OT = 13 cm है तथा OT वृत्त को E पर प्रतिच्छेद करती है। यदि AB, बिंदु E पर वृत्त की एक स्पर्श रेखा है तो AB की लंबाई ज्ञात कीजिए।
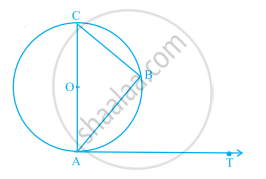
किसी वृत्त की बिंदु C पर खींची गई स्पर्श रेखा और व्यास AB बढ़ाने पर बिंदु P पर प्रतिच्छेद करते हैं। यदि ∠PCA = 110° है, तो ∠CBA ज्ञात कीजिए।