Advertisements
Advertisements
Question
आयत के विकर्ण परस्पर समकोण पर समद्विभाजित करते हैं।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण:
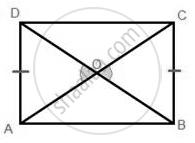
⇒ आयत ABCD में, विकर्ण कोणों को समद्विभाजित करते हैं।
ΔAOD और ΔBOC पर विचार करें
⇒ AD = BC ...(ABCD एक आयत है।)
⇒ ∠AOD = ∠BOC ...(ऊर्ध्वाधरतः विपरीत कोण)
⇒ ∠OAD = ∠OCB = 45° ...(विकर्ण कोणों को समद्विभाजित करते हैं।)
⇒ ΔAOD ≅ ΔBOC ...(AAS सर्वांगसमता कसौटी)
इसलिए, OA = OC और OB = OD
इस प्रकार विकर्ण एक दूसरे को आयत में समद्विभाजित करते हैं।
APPEARS IN
RELATED QUESTIONS
सभी वर्ग सम चतुर्भुज और आयत भी होते है।
ABC एक समकोण त्रिभुज है और 'O' समकोण की सम्मुख भुजा का मध्य - बिंदु है। बताइए कैसे 'O' बिंदु A, B तथा C से समान दुरी पर स्थित है। (बिंदुओं से चिन्हित अतिरिक्त भुजाएँ आपकी आपकी सहायता के लिए खींची गई है)
एक आयत, जिसकी भुजाएँ 10 cm और 24 cm हैं, के एक विकर्ण की लंबाई है –
आयत के विकर्ण ______ होते हैं।
यदि एक आयत के एक विकर्ण की लंबाई 6 cm हो, तो उसके दूसरे विकर्ण की लंबाई ______ होगी।
आयत के विकर्ण बराबर होते हैं।
एक फोटो फ्रेम एक चतुर्भुज के आकार का है। इसका एक विकर्ण दूसरे से बड़ा है। क्या यह एक आयत है? क्यों और क्यों नहीं?
