Question

ΔABC ∼ ΔPBQ, ΔABC मध्ये, AB = 4 सेमी, BC = 5 सेमी, AC = 6 सेमी. त्रिकोणाच्या संगत बाजूंचे गुणोत्तर 2:3 असल्यास ΔPBQ काढा.

Answer 1

विश्लेषण: 

 

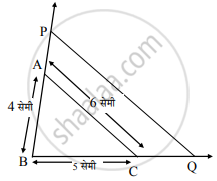
कच्ची आकृती

आकृतीत दाखवल्याप्रमाणे,

समजा, B – A – P व B – C – Q.

ΔABC ∼ ΔPBQ ..............[पक्ष]

∴ ∠ABC ≅ ∠PBQ ..........[सामाईक कोन]

`"AB"/"PB" = "BC"/"BQ" = "AC"/"PQ"` .............. [समरूप त्रिकोणांच्या संगत बाजू]

∴ `"AB"/"PB" = "BC"/"BQ" = "AC"/"PQ" = 2/3` 

∴ ΔPBQ च्या बाजू ΔABC च्या संगत बाजूंपेक्षा मोठ्या आहेत.

∴ जर रेख BC चे 2 समान भाग केले, तर त्यांतील एका भागाच्या 3 पट रेख BQ असेल.

म्हणून, जर ΔPBQ काढला, तर बिंदू C हा किरण BC वर B पासून 2 भाग अंतरावर असेल व बिंदू Q हा किरण BC वर B पासून 3 भाग अंतरावर असेल. आता, बिंदू Q मधून AC ला समांतर काढलेली रेषा व किरण BA यांचा छेदनबिंदू P हा आहे.

ΔPBQ हा ΔABC शी समरूप असणारा इष्ट त्रिकोण आहे.

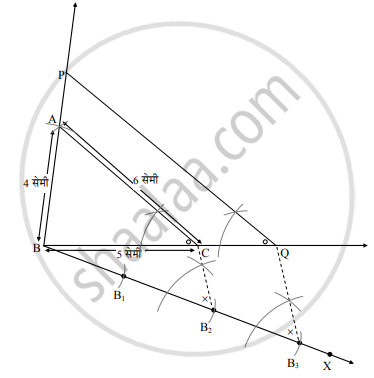
रचनेच्या पायऱ्या: 

1. दिलेल्या मापाचा ΔABC काढा. बाजू BC शी लघुकोन करणारा किरण BX काढा.
2. कंपासमध्ये सोयीस्कर अंतर घेऊन B₁, B₂ व B₃ हे 3 बिंदू असे घ्या, की BB₁ = B₁B₂ = B₂B₃ 
3. B₂C जोडा. B₃ मधून B₂C ला समांतर रेषा काढा. ही रेषा किरण BC ला Q बिंदूत छेदते.
4. बिंदू Q मधून AC ला समांतर रेषा काढा. ही रेषा व किरण BA यांच्या छेदनबिंदूला P नाव द्या.

ΔPBQ हा ΔABC शी समरूप असणारा इष्ट त्रिकोण आहे.