Advertisements
Advertisements
Question
बिंदु A(3, 1), B(12, –2) और C(0, 2) एक त्रिभुज के शीर्ष नहीं हो सकते।
Options
सत्य
असत्य
Solution
यह कथन सत्य है।
स्पष्टीकरण:
A के निर्देशांक = (x1, y1) = (3, 1)
B के निर्देशांक = (x2, y2) = (12, – 2)
C के निर्देशांक = (x3, y3) = (0, 2)
∆ABC का क्षेत्रफल = ∆ = `1/2[x_1 (y_2 - y_3) + x_2 (y_3 - y_1) + x_3 (y_1 - y_2)]`
Δ = `1/2 [3 - (2 - 2) + 12(2 - 1) + 0{1 - (- 2)}]`
Δ = `1/2 [3(- 4) + 12(1) + 0]`
Δ = `1/2 (- 12 + 12)` = 0
ΔABC का क्षेत्रफल = 0
चूँकि, बिंदु A(3, 1), B(12, – 2) और C(0, 2) संरेख हैं।
इसलिए, बिंदु A(3, 1), B(12, – 2) और C(0, 2) त्रिभुज के शीर्ष नहीं हो सकते।
APPEARS IN
RELATED QUESTIONS
उस चतुर्भुज का क्षेत्रफल ज्ञात कीजिए जिसके शीर्ष इसी क्रम में, (-4, -2), (-3, -5), (3, -2) और (2, 3) हैं।
निम्नलिखित में से प्रत्येक में 'k' का मान ज्ञात कीजिए, ताकि तीनों बिंदु संरेखी हों:
(8, 1), (k, -4), (2, -5)
कृष्णानगर के एक सेकेंडरी स्कूल के कक्षा X के विद्यार्थियों को उनके बागवानी क्रियाकलाप के लिए, एक आयताकार भूखंड दिया गया है। गुलमोहर की पौध (sapling) को परस्पर 1m की दूरी पर इस भूखंड की परिसीमा (boundary) पर लगाया जाता है। इस भूखंड के अंदर एक त्रिभुजाकार घास लगा हुआ लॉन (lawn) है, जैसाकि आकृति में दर्शाया गया है। विद्यार्थियों को भूखंड के शेष भाग में है फूलों के पौधे के बीज बोने हैं।
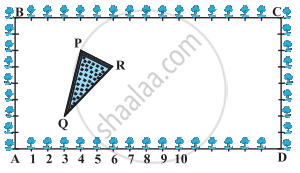
(i) A को मूलबिंदु मानते हए, त्रिभुज के शीषों के निर्देशांक ज्ञात कीजिए।
(ii) यदि मूलबिंदु C हो, तो ∆PQR के शीर्षों के निर्देशांक क्या होंगे?
साथ ही, उपरोक्त दोनों स्थितियों में, त्रिभुजों के क्षेत्रफल ज्ञात कीजिए। आप क्या देखते हैं?
बिंदुओं A(-1, -1), B(-1, 4), C(5, 4) और D(5, -1) से एक आयत ABCD बनता है। P, Q, R और S क्रमशः भुजाओं AB, BC, CD और DA के मध्य-बिंदु हैं। क्या चतुर्भुज PQRS एक वर्ग है? क्या यह एक आयत है? क्या यह एक समचतुर्भुज है? सकारण उत्तर दीजिए।
शीर्षों (a, b + c), (b, c + a) और (c, a + b) वाले त्रिभुज का क्षेत्रफल ______ हैं।
बिंदु (0, 5), (0, –9) और (3, 6) संरेख हैं।
A(6, 1), B(8, 2) और C(9, 4) एक समांतर चतुर्भुज ABCD के तीन शीर्ष हैं। यदि E भुजा DC का मध्य-बिंदु है, तो ΔADE का क्षेत्रफल ज्ञात कीजिए।
एक समद्विबाहु समकोण त्रिभुज का क्षेत्रफल 8 cm2 है। इसके कर्ण की लंबाई है।
एक समबाहु त्रिभुज का परिमाप 60 m है। इसका क्षेत्रफल है
एक समलंब का क्षेत्रफल 475 cm2 है तथा ऊँचाई 19 cm है। इसकी समांतर भुजाओं की लंबाइयाँ ज्ञात कीजिए, यदि एक समांतर भुजा दूसरी समांतर भुजा से 4 cm अधिक है।
