Advertisements
Advertisements
Question
Can a process on an ideal gas be both adiabatic and isothermal?
Solution
According to the first law of thermodynamics, change in internal energy, ΔU is equal to the difference between heat supplied to the gas, Δ Q and the work done on the gas, ΔW,
such that ΔQ = ΔU +ΔW . In an adiabatic process, ΔQ =0 and in an isothermal process, change in temperature, Δ T =0. Therefore,
ΔQ = ΔU + ΔW
⇒ ΔQ = nCvΔT +ΔW
⇒ 0 =nCv(0) + Δ W
⇒ Δ W = 0 ,
if the process is adiabatic as well as isothermal, no work will be done. So, a process on an ideal gas cannot be both adiabatic and isothermal.
APPEARS IN
RELATED QUESTIONS
The specific heat capacity of water is
Does a gas have just two specific heat capacities or more than two? Is the number of specific heat capacities of a gas countable?
Does a solid also have two kinds of molar heat capacities Cp and Cv? If yes, is Cp > Cv? Or is Cp − Cv = R?
In a real gas, the internal energy depends on temperature and also on volume. The energy increases when the gas expands isothermally. Examining the derivation of Cp − Cv = R, find whether Cp − Cv will be more than R, less than R or equal to R for a real gas.
Can two states of an ideal gas be connected by an isothermal process as well as an adiabatic process?
Let ∆Wa and ∆Wb be the work done by the systems A and B, respectively, in the previous question.
5 g of a gas is contained in a rigid container and is heated from 15°C to 25°C. Specific heat capacity of the gas at constant volume is 0.172 cal g−1 °C−1 and the mechanical equivalent of heat is 4.2 J cal−1. Calculate the change in the internal energy of the gas
A sample of air weighing 1.18 g occupies 1.0 × 103 cm3 when kept at 300 K and 1.0 × 105 Pa. When 2.0 cal of heat is added to it at constant volume, its temperature increases by 1°C. Calculate the amount of heat needed to increase the temperature of air by 1°C at constant pressure if the mechanical equivalent of heat is 4.2 × 107 erg cal−1. Assume that air behaves as an ideal gas.
An ideal gas expands from 100 cm3 to 200 cm3 at a constant pressure of 2.0 × 105 Pa when 50 J of heat is supplied to it. Calculate (a) the change in internal energy of the gas (b) the number of moles in the gas if the initial temperature is 300 K (c) the molar heat capacity Cp at constant pressure and (d) the molar heat capacity Cv at constant volume.
A mixture contains 1 mole of helium (Cp = 2.5 R, Cv = 1.5 R) and 1 mole of hydrogen (Cp= 3.5 R, Cv = 2.5 R). Calculate the values of Cp, Cv and γ for the mixture.
Air (γ = 1.4) is pumped at 2 atm pressure in a motor tyre at 20°C. If the tyre suddenly bursts, what would be the temperature of the air coming out of the tyre? Neglect any mixing with the atmospheric air.
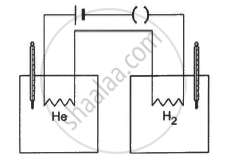
The figure shows two vessels with adiabatic walls, one containing 0.1 g of helium (γ = 1.67, M = 4 g mol−1) and the other containing some amount of hydrogen (γ = 1.4, M = 2 g mol−1). Initially, the temperatures of the two gases are equal. The gases are electrically heated for some time during which equal amounts of heat are given to the two gases. It is found that the temperatures rise through the same amount in the two vessels. Calculate the mass of hydrogen.
Standing waves of frequency 5.0 kHz are produced in a tube filled with oxygen at 300 K. The separation between the consecutive nodes is 3.3 cm. Calculate the specific heat capacities Cp and Cv of the gas.
An engine takes in 5 moles of air at 20°C and 1 atm, and compresses it adiabatically to `1/10^"th"` of the original volume. Assuming air to be a diatomic ideal gas made up of rigid molecules, the change in its internal energy during this process comes out to be X kJ. The value of X to the nearest integer is ______.
A diatomic molecule can be modelled as two rigid balls connected with spring such that the balls can vibrate with respect to centre of mass of the system (spring + balls). Consider a diatomic gas made of such diatomic molecule. If the gas performs 20 Joule of work under isobaric condition, then heat given to the gas is ______ J.
If at same temperature and pressure, the densities for two diatomic gases are respectively d1 and d2 then the ratio of velocities of sound in these gases will be ______.
