Advertisements
Advertisements
Question
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question: |
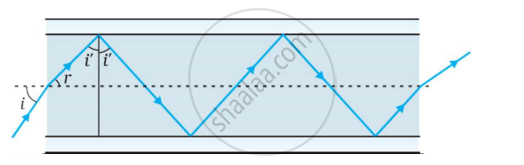
The following figure shows a cross-section of a ‘light pipe’ made of a glass fiber of refractive index 1.68. The outer covering of the pipe is made of a material of refractive index 1.44. What is the range of the angles of the incident rays with the axis of the pipe for the following phenomena to occur.
Options
0 < i < 90°
0 < i < 60°
0 < i < 45°
0 < i < 30°
Solution
0 < i < 60°
Explanation -
`1_(mu_2) = 1/(Sin "C'")`
Sin C' = `1.44/1.68` = 0.8571
C' ⇒ 59°
Total internal reflection will occur if the angle `"i'" > "i"_"c"^"'"`,
i.e., if i' > 59° or when r < rmax’ where rmax = 90° – 59° = 31°.
Using Snell’s law,
`("Sin" "i"_"max")/("Sin" "r"_"max")` = 1.68
or Sin imax = 1.68 × Sin rmax
= 1.68 × sin 31°
= 1.68 × 0.5150
= 0.8662
∴ imax = 60°
Thus all incident rays which make angles in the range 0 < i < 60° with the axis of the pipe will suffer total internal reflections in the pipe.
APPEARS IN
RELATED QUESTIONS
Draw the intensity distribution for the fringes produced in interference ?
A concave mirror has a focal length of 20 cm. Find the position or positions of an object for which the image-size is double of the object-size.
A 3 cm tall object is placed at a distance of 7.5 cm from a convex mirror of focal length 6 cm. Find the location, size and nature of the image.
k transparent slabs are arranged one over another. The refractive indices of the slabs are μ1, μ2, μ3, ... μk and the thicknesses are t1 t2, t3, ... tk. An object is seen through this combination with nearly perpendicular light. Find the equivalent refractive index of the system which will allow the image to be formed at the same place.
A container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water = 4/3.
The diameter of the sun is 1.4 × 109 m and its distance from the earth is 1.5 × 1011 m. Find the radius of the image of the sun formed by a lens of focal length 20 cm.
Rainbow is the phenomenon due to ______.
Explain the formation of primary and secondary rainbow.
A parallel beam of light of wavelength 5890 Å falls normally on a slit of width 0.2 mm. Find the distance between the first minima on the two sides of the central maximum of the diffraction pattern observed on a screen placed in the focal plane of a convex lens of focal length 50 cm. The lens is placed quite close to the slit.
| Case study: Mirage in deserts |
 |
|
To a distant observer, the light appears to be coming from somewhere below the ground. The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts. Based on the above facts, answer the following question : |
In an optical fibre, if n1 and n2 are the refractive indices of the core and cladding, then which among the following, would be a correct equation?
