Advertisements
Advertisements
Question
Consider a particle moving in simple harmonic motion according to the equation x = 2.0 cos (50 πt + tan−1 0.75) where x is in centimetre and t in second. The motion is started at t = 0. (a) When does the particle come to rest for the first time? (b) When does he acceleration have its maximum magnitude for the first time? (c) When does the particle come to rest for the second time ?
Solution
It is given that a particle executes S.H.M.
Equation of S.H.M. of the particle:
x = 2.0 cos (50 \[\pi\] t + tan−10.75)
= 2.0 cos (50 \[\pi\]t + 0.643)
(a) Velocity of the particle is given by,
\[v = \frac{\text {dx}}{\text{dt}}\]
v = −100 \[\pi\]sin (50 \[\pi\]t + 0.643)
As the particle comes to rest, its velocity becomes be zero.
⇒ v = −100 \[\pi\]sin (50 \[\pi\]t + 0.643) = 0
⇒ sin (50\[\pi\]t + 0.643) =0 = sin\[\pi\]
When the particle initially comes to rest,
50\[\pi\]t + 0.643 =\[\pi\]
⇒ t = 1.6 × 10−2 s
(b) Acceleration is given by,
\[a = \frac{dv}{dt}\]
\[ = - 100\pi \times 50\pi \cos \left( 50\pi t + 0 . 643 \right)\]
For maximum acceleration:
cos (50\[\pi\]t + 0.643) = −1 = cos\[\pi\](max) (so that a is max)
=> t = 1.6 × 10−2 s
(c) When the particle comes to rest for the second time, the time is given as,
50\[\pi\]t + 0.643 = 2\[\pi\]
⇒ t = 3.6 × 10−2 s
APPEARS IN
RELATED QUESTIONS
A particle executes simple harmonic motion with an amplitude of 10 cm. At what distance from the mean position are the kinetic and potential energies equal?
The equation of motion of a particle started at t = 0 is given by x = 5 sin (20t + π/3), where x is in centimetre and t in second. When does the particle
(a) first come to rest
(b) first have zero acceleration
(c) first have maximum speed?
The pendulum of a clock is replaced by a spring-mass system with the spring having spring constant 0.1 N/m. What mass should be attached to the spring?
A body of mass 2 kg suspended through a vertical spring executes simple harmonic motion of period 4 s. If the oscillations are stopped and the body hangs in equilibrium find the potential energy stored in the spring.
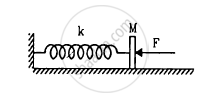
In following figure k = 100 N/m M = 1 kg and F = 10 N.
- Find the compression of the spring in the equilibrium position.
- A sharp blow by some external agent imparts a speed of 2 m/s to the block towards left. Find the sum of the potential energy of the spring and the kinetic energy of the block at this instant.
- Find the time period of the resulting simple harmonic motion.
- Find the amplitude.
- Write the potential energy of the spring when the block is at the left extreme.
- Write the potential energy of the spring when the block is at the right extreme.
The answer of b, e and f are different. Explain why this does not violate the principle of conservation of energy.
Repeat the previous exercise if the angle between each pair of springs is 120° initially.
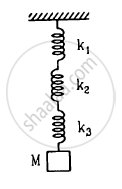
Find the elastic potential energy stored in each spring shown in figure, when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
Solve the previous problem if the pulley has a moment of inertia I about its axis and the string does not slip over it.
Find the elastic potential energy stored in each spring shown in figure when the block is in equilibrium. Also find the time period of vertical oscillation of the block.
Discuss in detail the energy in simple harmonic motion.
Show that for a particle executing simple harmonic motion.
- the average value of kinetic energy is equal to the average value of potential energy.
- average potential energy = average kinetic energy = `1/2` (total energy)
Hint: average kinetic energy = <kinetic energy> = `1/"T" int_0^"T" ("Kinetic energy") "dt"` and
average potential energy = <potential energy> = `1/"T" int_0^"T" ("Potential energy") "dt"`
When a particle executing S.H.M oscillates with a frequency v, then the kinetic energy of the particle?
When the displacement of a particle executing simple harmonic motion is half its amplitude, the ratio of its kinetic energy to potential energy is ______.
A body is executing simple harmonic motion with frequency ‘n’, the frequency of its potential energy is ______.
Motion of an oscillating liquid column in a U-tube is ______.
Find the displacement of a simple harmonic oscillator at which its P.E. is half of the maximum energy of the oscillator.
A mass of 2 kg is attached to the spring of spring constant 50 Nm–1. The block is pulled to a distance of 5 cm from its equilibrium position at x = 0 on a horizontal frictionless surface from rest at t = 0. Write the expression for its displacement at anytime t.
