Advertisements
Advertisements
Question
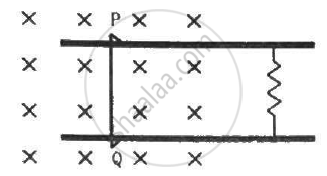
Consider the situation shown in figure. The wire PQ has mass m, resistance r and can slide on the smooth, horizontal parallel rails separated by a distance l. The resistance of the rails is negligible. A uniform magnetic field B exists in the rectangular region and a resistance R connects the rails outside the field region. At t = 0, the wire PQ is pushed towards right with a speed v0. Find (a) the current in the loop at an instant when the speed of the wire PQ is v, (b) the acceleration of the wire at this instant, (c) the velocity vas a functions of x and (d) the maximum distance the wire will move.
Solution
(a) When wire PQ is moving with a speed v, the emf induced across it is given by
e = Blv
Total resistance of the circuit = r + R
∴ Current in the circuit, \[i = \frac{Blv}{r + R}\]
(b) Force acting on the wire at the given instant, F = ilB
On substituting the value of i from above, we get
\[F = \frac{(Blv)(lB)}{(R + r)} = \frac{B^2 l^2 v}{R + r}\]
Acceleration of the wire is given by
\[a= \frac{B^2 l^2 v}{m (R + r)}\]
(c) Velocity can be expressed as:-
\[v = v_0 + at = v_0 - \frac{B^2 l^2 v}{m (R + r)}t..........\left(\text{As force is opposite to velocity}\right)\]
Velocity as the function of x is given by
\[v = v_0 - \frac{B^2 l^2 x}{m (R + r)}\]
(d) \[a = v\frac{dv}{dx} = \frac{B^2 l^2 v}{m (R + r)}\]
\[dx = \frac{m (R + r)}{B^2 l^2}dv\]
On integrating both sides, we get
\[x = \frac{m(R + r) v_0}{B^2 l^2}\]
APPEARS IN
RELATED QUESTIONS
Find the condition under which the charged particles moving with different speeds in the presence of electric and magnetic field vectors can be used to select charged particles of a particular speed.
Depict the behaviour of magnetic field lines in the presence of a diamagnetic material?
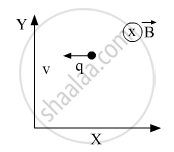
A point charge q moving with speed v enters a uniform magnetic field B that is acting into the plane of the paper as shown. What is the path followed by the charge q and in which plane does it move?
If an electric field \[\vec{E}\] is also applied such that the particle continues moving along the original straight line path, what should be the magnitude and direction of the electric field \[\vec{E}\] ?
Show with the help of a diagram how the force between the two conductors would change when the currents in them flow in the opposite directions?
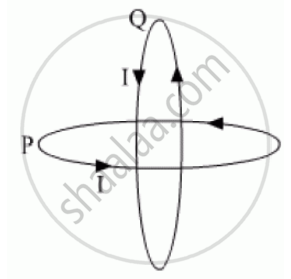
Two identical circular wires P and Q each of radius R and carrying current ‘I’ are kept in perpendicular planes such that they have a common centre as shown in the figure. Find the magnitude and direction of the net magnetic field at the common centre of the two coils.
Two long straight parallel conductors carrying steady currents I1 and I2 are separated by a distance 'd'. Explain briefly, with the help of a suitable diagram, how the magnetic field due to one conductor acts on the other. Hence deduce the expression for the force acting between the two conductors. Mention the nature of this force.
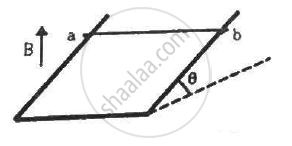
A wire ab of length l, mass m and resistance R slides on a smooth, thick pair of metallic rails joined at the bottom as shown in figure. The plane of the rails makes an angle θ with the horizontal. A vertical magnetic field B exists in the region. If the wire slides on the rails at a constant speed v, show that \[B = \sqrt{\frac{mg R sin\theta}{v l^2 \cos^2 \theta}}\]
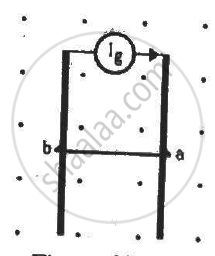
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire ab has a length l and mass m and can slide on the smooth, horizontal rails connected to Ig. The entire system lies in a vertical magnetic field B. The system is kept vertically in a uniform horizontal magnetic field B that is perpendicular to the plane of the rails (figure). It is found that the wire stays in equilibrium. If the wire ab is replaced by another wire of double its mass, how long will it take in falling through a distance equal to its length?
A magnetic field that varies in magnitude from point to point but has a constant direction (east to west) is set up in a chamber. A charged particle enters the chamber and travels undeflected along a straight path with constant speed. What can you say about the initial velocity of the particle?
A charged particle moves through a magnetic field perpendicular to its direction. Then ______.
A circular coil of radius 10 cm is placed in a uniform magnetic field of 3.0 × 10-5 T with its plane perpendicular to the field initially. It is rotated at constant angular speed about an axis along the diameter of coil and perpendicular to magnetic field so that it undergoes half of rotation in 0.2 s. The maximum value of EMF induced (in µV) in the coil will be close to the integer ______.
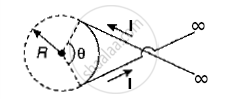
A wire carrying current i has the configuration shown in figure. For the magnetic field to be zero at the centre of the circle, θ must be:
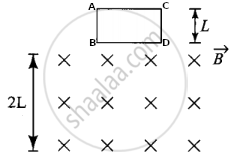
A square coil ABCD with its plane vertical is released from rest in a horizontal uniform magnetic field `vec"B"` of length 2L. The acceleration of the coil is ______.
An α particle is moving along a circle of radius R with a constant angular velocity ω. Point A lies in the same plane at a distance 2R from the centre. Point A records magnetic field produced by α particle, if the minimum time interval between two successive times at which A records zero magnetic field is 't' the angular speed ω, in terms of t is ______.
A charged particle is accelerated through a potential difference of 12 kV and acquires a speed of 106 ms-1. It is projected perpendicularly into the magnetic field of strength 0.2 T. The radius of the circle described is ______ cm.
A charge Q is moving `vec"dl"` distance in the magnetic field `vec"B"`. Find the value of work done by `vec"B"`.
Protons and singly ionized atoms of U235 and U238 are passed in turn (which means one after the other and not at the same time) through a velocity selector and then enter a uniform magnetic field. The protons describe semicircles of radius 10 mm. The separation between the ions of U235 and U238 after describing the semicircle is given by ______.
