Advertisements
Advertisements
Question
Draw a line AB = 5 cm. Mark a point C on AB such that AC = 3 cm. Using a ruler and a compass only, construct :
- A circle of radius 2.5 cm, passing through A and C.
- Construct two tangents to the circle from the external point B. Measure and record the length of the tangents.
Solution
Steps for construction:
- Draw AB = 5 cm using a ruler.
- With A as the centre cut an arc of 3 cm on AB to obtain C.
- With A as the centre and radius 2.5 cm, draw an arc above AB.
- With same radius and C as the centre draw an arc to cut the previous arc and mark the intersection as O.
- With O as the centre and radius 2.5 cm, draw a circle so that points A and C lie on the circle formed.
- Join OB.
- Draw the perpendicular bisector of OB to obtain the mid-point of OB, M.
- With the M as the centre and radius equal to OM, draw a circle to cut the previous circle at points P and Q.
- Join PB and QB. PB and QB are the required tangents to the given circle from exterior point B.
QB = PB = 3 cm
That is, length of the tangents is 3 cm.

APPEARS IN
RELATED QUESTIONS
Draw a line segment AB of length 8 cm. Taking A as centre, draw a circle of radius 4 cm and taking B as centre, draw another circle of radius 3 cm. Construct tangents to each circle from the centre of the other circle.
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
Draw a circle of radius 6 cm. From a point 10 cm away from its centre, construct the pair of tangents to the circle and measure their lengths. Give the justification of the construction.
Draw an inscribing circle of a regular hexagon of side 5.8 cm.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
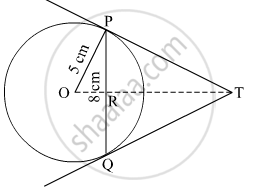
In Figure 2, PQ is a chord of length 8 cm of a circle of radius 5 cm. The tangents at P and Q intersect at a point T. Find the length TP.
Draw a circle at a radius of 4 cm. Take a point on it. Without using the centre at the circle, draw a tangent to the circle at point P.
Draw an isosceles triangle with sides 6 cm, 4 cm, and 6 cm. Construct the incircle of the triangle. Also, write the steps of construction.
A pair of tangents can be constructed from a point P to a circle of radius 3.5 cm situated at a distance of 3 cm from the centre.
