Advertisements
Advertisements
Question
Draw a circle of radius 4.2. Draw a pair of tangents to this circle inclined to each other at an angle of 45°
Solution
Steps of Construction:
Step 1: Draw a circle with center O and radius = 4.2 cm.
Step 2: Draw any diameter AOB of this circle.
Step 3: Construct ∠BOC = 45°. such that the radius OC meets the circle at C.
Step4: Draw AM ⊥ AB and CN ⊥ OC.
AM and CN intersect at P.
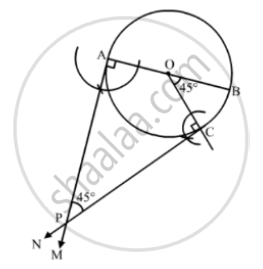
Thus, PA and PC are the required tangents to the given circle inclined at an angle of 45°.
APPEARS IN
RELATED QUESTIONS
Construct a tangent to a circle of radius 4 cm from a point on the concentric circle of radius 6 cm and measure its length. Also verify the measurement by actual calculation.
Draw a pair of tangents to a circle of radius 5 cm which are inclined to each other an angle of 60º.
Construct a circle, inscribing an equilateral triangle with side 5.6 cm.
Draw a circle of radius 3.5 cm. Take two points A and B on one of its extended diameter, each at a distance of 5 cm from its center. Draw tangents to the circle from each of these points A and B.
Draw a circle of radius 32 cm. Draw a tangent to the circle making an angle 30° with a line passing through the centre.
Draw two concentric circles with radii 4 cm and 6 cm. Taking a point on the outer circle, construct a pair of tangents to inner circle. By measuring the lengths of both the tangents, show that they are equal to each other.
Draw a circle of radius 4 cm. From a point 6 cm away from its centre, construct a pair of tangents to the circle and measure their lengths.
Draw a circle at a radius of 3 cm. Take a point at 5.5 cm from the center at the circle. From point P, draw two tangents to the circle.
Draw a circle of radius 3 cm and construct a tangent to it from an external point without using the center.
A pair of tangents can be constructed from a point P to a circle of radius 3.5cm situated at a distance of ______ from the centre.
