Advertisements
Advertisements
Question
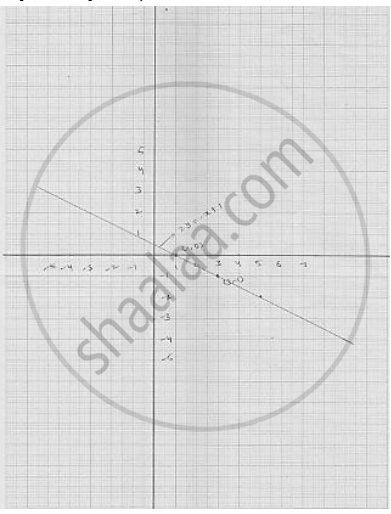
Draw the graph of the following linear equations in two variable : 2𝑦 = −𝑥 + 1
Solution
we have
`2y = -x + 1`
⇒ x -1 = 2y ............. (1)
Putting y = 0 , we get x = 1 - 2 × 0 = 1
Putting y = -1 , we get x = 1 - 2 ( - 1) = 3
Thus, we have the following table giving the two points on the line represented by
the equation
2y = x - 3
2y = - x + 1
Graph for the equation 2y = - x +1
APPEARS IN
RELATED QUESTIONS
Draw the graph of the following linear equation in two variable : `(x-2)/3 = y - 3`
If the point (2, -2) lies on the graph of the linear equation 5x + ky = 4, find the value of k.
Draw the graph of y = | x |.
Draw the graph for the equation given below; hence find the co-ordinates of the points where the graph is drawn meets the co-ordinates axes:
`(2x + 15)/(3) = y - 1`
Draw the graph of the straight line given by the equation 4x - 3y + 36 = 0
Calculate the area of the triangle formed by the line drawn and the co-ordinate axes.
Draw the graph of the equation
4x + 3y + 6 = 0
From the graph, find :
(i) y1, the value of y, when x = 12.
(ii) y2, the value of y, when x = - 6.
Use graph paper for this question. Draw the graph of 2x - y - 1 = 0 and 2x + y = 9 on the same axes. Use 2 cm = 1 unit on both axes and plot only 3 points per line. Write down the coordinates of the point of intersection of the two lines.
Use graph paper for this question. Take 2 cm = 1 unit on both the axes.
- Draw the graphs of x + y + 3 = 0 and 3x - 2y + 4 = 0. Plot only three points per line.
- Write down the coordinates of the point of intersection of the lines.
- Measure and record the distance of the point of intersection of the lines from the origin in cm.
The graph of y = 6 is a line ______.
The force exerted to pull a cart is directly proportional to the acceleration produced in the body. Express the statement as a linear equation of two variables and draw the graph of the same by taking the constant mass equal to 6 kg. Read from the graph, the force required when the acceleration produced is (i) 5 m/sec2, (ii) 6 m/sec2.
