Advertisements
Advertisements
Question
दर्शाइए कि किसी समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
Solution
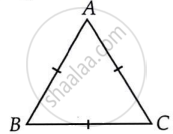
मान लीजिए ABC एक समबाहु त्रिभुज है।
∴ AB = BC = AC ...(A)
AB = BC ...[पहला तथा दूसरा पद लेने पर]
⇒ ∠C = ∠A …(i) ...[समान भुजाओं के सम्मुख कोण]
इसलिए,
AB = AC ...[(A) का पहला तथा तीसरा पद लेने पर]
⇒ ∠C = ∠B …(ii) ...[समान भुजाओं के सम्मुख कोण]
(i) और (ii) से हमें प्राप्त होता है।
∠A = ∠B = ∠C …(iii)
अब △ABC में …(iv)
∠A + ∠B + ∠C = 180° ...[कोण योगफल गुण]
⇒ ∠A + ∠A + ∠A = 180°
⇒ 3∠A = 180
⇒ ∠A = 60°
(iii) से, ∠A = ∠B = ∠C
⇒ ∠A = ∠B = ∠C = 60°
अतः, समबाहु त्रिभुज का प्रत्येक कोण 60° होता है।
APPEARS IN
RELATED QUESTIONS
एक समद्विबाहु त्रिभुज ABC में जिसमें AB = AC है, ∠B और ∠C के समद्विभाजक परस्पर बिंदु O पर प्रतिच्छेद करते हैं। A और O को जोड़िए। दर्शाइए कि:
- OB = OC
- AO कोण A को समद्विभाजित करता है।
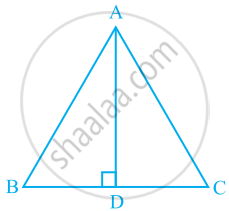
△ABC में, AD भुजा BC का लम्ब समद्विभाजक है (देखिए आकृति)। दर्शाइए △ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है।
ABC एक समद्विबाहु त्रिभुज है, जिसमें बराबर भुजाओं AC और AB पर क्रमशः शीर्षलंब BE और CF खींचे गए हैं (देखिए आकृति)। दर्शाइए कि ये शीर्षलंब बराबर हैं।
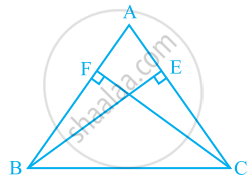
ABC एक त्रिभुज है जिसमें AC और AB पर खींचे गए शीर्षलंब BE और CF बराबर हैं (देखिए आकृति)। दर्शाइए कि
- △ABE ≌ △ACF
- AB = AC, अर्थात् △ABC एक समद्विबाहु त्रिभुज है।

ABC और DBC समान आधार BC पर स्थित दो समद्विबाहु त्रिभुज हैं (देखिए आकृति)। दर्शाइए कि
∠ABD = ∠ACD है।
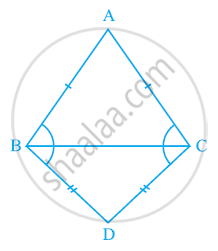
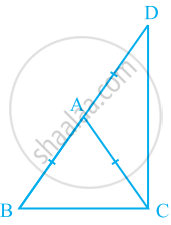
ABC एक समद्विबाहु त्रिभुज है, जिसमें AB = AC है। भुजा BA बिंदु D तक इस प्रकार बढ़ाई गई है कि AD = AB है (देखिए आकृति)। दर्शाइए कि ∠BCD एक समकोण है।
D एक त्रिभुज ABC की भुजा BC पर एक बिंदु इस प्रकार स्थित है कि AD कोण BAC को समद्विभाजित करता है। तब, ______
त्रिभुजों ABC और DEF में, AB = FD तथा ∠A = ∠D है। दोनों त्रिभुज SAS अभिगृहीत से सर्वांगसम होंगे, यदि ______।
CDE एक वर्ग ABCD की भुजा CD पर बना एक समबाहु त्रिभुज है (आकृति)। दर्शाइए कि ∆ADE ≅ ∆BCE है।

एक ∆PSR की भुजा SR पर एक बिंदु Q इस प्रकार स्थित है कि PQ = PR है। सिद्ध कीजिए कि PS > PQ है।
