Advertisements
Advertisements
Question
एक त्रिभुज ABC के शीर्षों के निर्देशांक क्रमशः A(0, 0, 6), B(0, 4, 0) तथा C(6, 0, 0) हैं। त्रिभुज की माध्यिकाओं की लंबाई ज्ञात कीजिए।
Solution
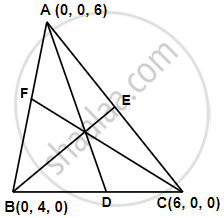
बिंदु B(0, 4, 0) और C(6, 0, 0) को मिलाने वाला रेखाखंड का मध्य बिंदु D `((0 + 6)/2, (4 + 0)/2, (0 + 0)/2)` या (3, 2, 0) हैं।
∴ बिंदु A के निर्देशांक (0, 0, 6) हैं।
त्रिभुज ABC की माध्यिका AD की लंबाई
= `sqrt((3 - 0)^2 + (2 - 0)^2 + (0 - 6)^2)`
= `sqrt(9 + 4 + 36)`
= `sqrt49`
= 7
C और A के निर्देशांक (6, 0, 0) और (0, 0, 6)
AC का मध्य बिंदु E `((0 + 6)/2, (0 + 0)/2, (0 + 6)/2)` या E (3, 0, 3)
और B के निर्देशांक (0, 4, 0) हैं।
त्रिभुज ABC की माध्यिका BE की लंबाई
= `sqrt((3 - 0)^2 + (0 - 4)^2 + (3 - 0)^2)`
= `sqrt(9 + 16 + 9)`
= `sqrt34`
बिंदु A और B के निर्देशांक क्रमशः (0, 0, 6), (0, 4, 0) हैं।
∴ AB का मध्य बिंदु F`((0 + 0)/2, (0 + 4)/2, (6 + 0)/2)` या F (0, 2, 3) हैं।
त्रिभुज ABC की माध्यिका CF की लंबाई
= `sqrt((6 - 0)^2 + (0 - 2)^2 + (0 + 3)^2)`
= `sqrt(36 + 4 + 9)`
= `sqrt49`
= 7
APPEARS IN
RELATED QUESTIONS
y-अक्ष पर उस बिंदु के निर्देशांक ज्ञात कीजिए जिसकी बिंदु P(3, –2, 5) से दूरी `5sqrt2` है।
P(2, –3, 4) और Q(8, 0, 10) को मिलाने वाली रेखाखंड पर स्थित एक बिंदु R का x-निर्देशांक 4 है। बिंदु R के निर्देशांक ज्ञात कीजिए।
(संकेत: मान लीजिए R, PQ को k : 1 में विभाजित करता है। बिंदु R के निर्देशांक `((8"k" + 2)/("k" + 1), (-3)/("k" + 1), (10"k" + 4)/("k" + 1))` हैं।)
यदि बिंदु A और B क्रमशः (3, 4, 5) तथा (−1, 3, –7) हैं। चर बिंदु P द्वारा निर्मित समुच्चय से संबंधित समीकरण ज्ञात कीजिए, जहाँ PA2 + PB2 = k2 जब कि k अचर है।
