Question

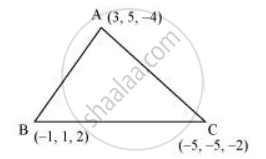
एक त्रिभुज की भुजाओं की दिक्-कोसाइन ज्ञात कीजिए यदि त्रिभुज के शीर्ष बिंदु (3, 5, −4), (−1, 1, 2) और (−5, –5, –2) हैं।

Answer 1

मान लीजिए, A(3, 5,−4), B(−1, 1, 2) और C(−5, −5, −2) हैं।

AB का दिक्-अनुपात = (−1 − 3), (1 − 5), (2 − (−4))

= (−4, −4, 6)

|AB| = `sqrt((-4)^2 + (-4)^2 + (6)^2)`

= `sqrt(16 + 16 + 36)`

= `sqrt68`

= `2sqrt17`

BC का दिक्-अनुपात = (−5 − (−1), −5 − 1, −2 − 2)

= (−4, −6, −4)

|BC| = `sqrt((-4)^2 + (-6)^2 + (-4)^2)`

= `sqrt(16 + 36 + 16)`

= `sqrt68`

= `2sqrt17`

CA का दिक्-अनुपात = (−5 − 3, −5 − 5, −2 − (−4))

= (−8, −10, 2)

|CA| = `sqrt((-8)^2 + (-10)^2 + (2)^2)`

= `sqrt(64 + 100 + 4)`

= `sqrt168`

= `2sqrt42`

∴ AB `< (-1 - 3)/|AB|, (1 - 5)/|AB|, (2 + 4)/|AB| `,

अर्थात, `< (-2)/sqrt17, (-2)/sqrt17, 3/sqrt17 >`

∴ BC `< (-5 + 1)/|BC|, (- 5 - 1)/|BC|, (- 2 -2)/|BC|>`

अर्थात, `< (-2)/sqrt17, (-3)/sqrt17, (-2)/sqrt17 >`

∴  CA `< (3 + 5)/|CA|, (5 + 5)/|CA|, (- 4 + 2)/|CA|`

अर्थात, `< 4/sqrt42, 5/sqrt42, (-1)/sqrt42 >`