Advertisements
Advertisements
Question
एक तुर्की टोपी शंकु के एक छिन्नक के आकार की है। यदि इसके खुले सिरे की त्रिज्या 10 सेमी है, ऊपरी सिरे की त्रिज्या 4 सेमी है और टोपी की तिर्यक ऊँचाई 15 सेमी है, तो इसके बनाने में प्रयुक्त पदार्थ का क्षेत्रफल ज्ञात कीजिए।
[उपयोग π = 22/7]

Solution
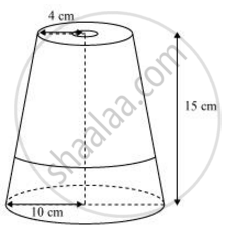
त्रिज्या (r2) ऊपरी वृत्ताकार सिरे पर = 4 सेमी
त्रिज्या (r1) निचले वृत्ताकार सिरे पर = 10 cm
छिन्नक की तिरछी ऊँचाई (l) = 15 cm
फेज बनाने में प्रयुक्त सामग्री का क्षेत्रफल = छिन्नक का CSA + ऊपरी वृत्ताकार सिरे का क्षेत्रफल
`= pi(r_1+r_2)l + pir_2^2`
= (10 + 4) 15 + (4) 2
= (14) 15 + 16
`= 210pi + 16pi = (226xx22)/7`
`= 710 2/7 "सेमी"^2`
अतः इसे बनाने में प्रयुक्त सामग्री का क्षेत्रफल `710 2/7 cm^2` है
APPEARS IN
RELATED QUESTIONS
पानी पीने वाला एक गिलास 14 सेमी ऊँचाई वाले एक शंकु के छिन्नक के आकार का है। दोनों वृत्ताकार सिरों के व्यास 4 सेमी और 2 सेमी हैं। इस गिलास की धारिता ज्ञात कीजिए। [उपयोग π = 22/7]
एक शंकु के छिन्नक की तिर्यक ऊँचाई 4 सेमी है तथा इसके वृत्तीय सिरों के परिमाप 18 सेमी और 6 सेमी हैं। इस छिन्नक का वक्र पृष्ठीय क्षेत्रफल ज्ञात कीजिए।
20 सेमी ऊँचाई और शीर्ष कोण 60 डिग्री वाले एक शंकु को उसकी ऊँचाई के बीचोबीच से होकर जाते हुए एक तल से दो भागों में काटा गया है, जबकि तल शंकु के आधार के समांतर है। यदि इस प्राप्त शंकु के छिन्नक को व्यास `1/16` सेमी वाले एक तार के रूप में बदल दिया जाता है तो तार की लंबाई ज्ञात कीजिए। [उपयोग π = `22/7`]
एक शंकु के छिन्नक के आयतन का सूत्र व्युत्पन्न कीजिए।
एक गिलास का आकार प्रायः निम्न रूप का होता है-

एक शंकु को उसके आधार के समांतर एक तल की सहायता से काटा जाता है और फिर तल के एक ओर बने शंकु को हटा दिया जाता है। तल के दूसरी ओर बचा हुआ नया भाग कहलाता है एक ______।
एक बाल्टी के दोनों वृत्ताकार सिरों के व्यास 44 cm और 24 cm हैं तथा बाल्टी की ऊँचाई 35 cm है। इस बाल्टी की धारिता ______ है।
एक लंब वृत्तीय शंकु में, उसके आधार के समांतर खींचे गये तल द्वारा काटा गया अनुप्रस्थ-काट होता है एक ______।
शंकु के एक छिन्नक का आयतन `1/3 pih[r_1^2 + r_2^2 - r_1r_2]` होता है, जहाँ h छिन्नक की ऊर्घ्वाधर ऊँचाई है और r1, r2 सिरों की त्रिज्याएँ हैं।
शंकु के एक छिन्नक का वक्र पृष्ठीय क्षेत्रफल πl (r1 + r2) होता है, जहाँ `l = sqrt(h^2 + (r_1 + r _2)^2)` है, r1 और r2 छिन्नक के दोनों सिरों की त्रिज्याएँ हैं तथा h ऊर्ध्वाधर ऊँचाई है।
