Advertisements
Advertisements
Question
Find the length a diagonal of a rectangle having sides 11 cm and 60 cm.
Solution

According to Pythagoras theorem,
In ∆ABC
\[{AB}^2 + {BC}^2 = {AC}^2 \]
\[ \Rightarrow \left( 60 \right)^2 + \left( 11 \right)^2 = {AC}^2 \]
\[ \Rightarrow 3600 + 121 = {AC}^2 \]
\[ \Rightarrow {AC}^2 = 3721\]
\[ \Rightarrow AC = 61 cm\]
Hence, the length of a diagonal of the rectangle is 61 cm.
RELATED QUESTIONS
In ∆ABC, point M is the midpoint of side BC. If, AB2 + AC2 = 290 cm2, AM = 8 cm, find BC.

Out of the following, which is the Pythagorean triplet?
Some question and their alternative answer are given. Select the correct alternative.
Altitude on the hypotenuse of a right angled triangle divides it in two parts of lengths 4 cm and 9 cm. Find the length of the altitude.
Height and base of a right angled triangle are 24 cm and 18 cm find the length of its hypotenuse
Some question and their alternative answer are given. Select the correct alternative.
In ∆ABC, AB = \[6\sqrt{3}\] cm, AC = 12 cm, BC = 6 cm. Find measure of ∠A.
Find the height of an equilateral triangle having side 2a.
Do sides 7 cm, 24 cm, 25 cm form a right angled triangle ? Give reason
In ∆ABC, seg AP is a median. If BC = 18, AB2 + AC2 = 260, Find AP.
Sum of the squares of adjacent sides of a parallelogram is 130 sq.cm and length of one of its diagonals is 14 cm. Find the length of the other diagonal.
Seg PM is a median of ∆PQR. If PQ = 40, PR = 42 and PM = 29, find QR.
Seg AM is a median of ∆ABC. If AB = 22, AC = 34, BC = 24, find AM
If hypotenuse of a right angled triangle is 5 cm, find the radius of
the circle passing through all vertices of the triangle.
In ΔPQR, seg PM is the median. If PM = 9, PQ2 + PR2 = 290, Find QR.
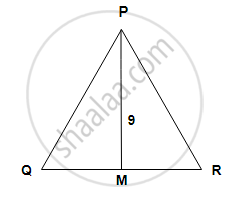
Choose the correct alternative:
Out of given triplets, which is not a Pythagoras triplet?
In the given figure, triangle ABC is a right-angled at B. D is the mid-point of side BC. Prove that AC2 = 4AD2 – 3AB2.

