Advertisements
Advertisements
Question
Find the remainder when x3 + 3x2 + 3x + 1 is divided by x.
Solution 1
Let p(x) = x3 + 3x2 + 3x + 1
x = 0
∴ Remainder = (0)3 + 3(0)2 + 3(0) + 1
= 1
Therefore, the remainder is 1.
Solution 2
By long division,
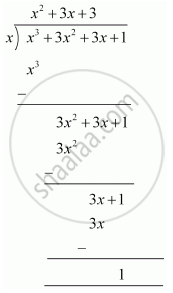
Therefore, the remainder is 1.
APPEARS IN
RELATED QUESTIONS
Check whether 7 + 3x is a factor of 3x3 + 7x.
Find 'a' if the two polynomials ax3 + 3x2 – 9 and 2x3 + 4x + a, leaves the same remainder when divided by x + 3.
If x3 + ax2 + bx + 6 has x – 2 as a factor and leaves a remainder 3 when divided by x – 3, find the values of a and b.
The expression 2x3 + ax2 + bx – 2 leaves remainder 7 and 0 when divided by 2x – 3 and x + 2 respectively. Calculate the values of a and b.
If (x – 2) is a factor of the expression 2x3 + ax2 + bx – 14 and when the expression is divided by (x – 3), it leaves a remainder 52, find the values of a and b.
Find the values of a and b when the factors of the polynomial f(x)= ax3 + bx2 + x a are (x+3) and (2x-1). Factorize the polynomial completely.
Find the remainder when the polynomial f(x) = 2x4 - 6x3 + 2x2 - x + 2 is divided by x + 2.
If p(x) = 4x3 - 3x2 + 2x - 4 find the remainderwhen p(x) is divided by:
x + `(1)/(2)`.
Find the remainder (without division) on dividing f(x) by (2x + 1) where f(x) = 4x2 + 5x + 3
What is the remainder when x2018 + 2018 is divided by x – 1
