Advertisements
Advertisements
Question
Find the area of a right-angled triangle whose hypotenuse is 13 cm long and one of its legs is 12 cm long.
Solution
In right-angled Δ ABC,
Base BC = 12 cm
and hypotenuse AC = 13 cm
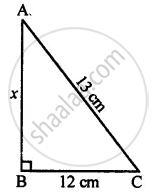
Applying Pythagoras Theorem,
(AC)2 = (AB)2 + (BC)2
(13)2 = (AB)2 + (12)2
169 = (AB)2 + 144
(AB)2 = 169 − 144
(AB)2 = 25
∴ AB =`sqrt25`
= `sqrt(5xx5)` = 5 cm
Now, area of Δ ABC =`1/2"base"xx"altitude"`
= `1/2xx12xx5` = 30 cm2
APPEARS IN
RELATED QUESTIONS
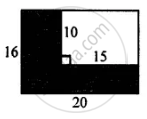
In the figure given below, find the area of shaded region: (All measurements are in cm)
The adjacent sides of a parallelogram are 15 cm and 10 cm. If the distance between the longer sides is 6 cm, find the distance between the shorter sides.
The area of a rhombus is 84 cm2 and its perimeter is 56 cm. Find its height.
Find the area of an isosceles triangle whose base is 16 cm and the length of each of the equal sides is 10 cm.
The legs of a right-angled triangle are in the ratio 4 : 3 and its area is 4056 cm2. Find the length of its legs.
The ratio between the areas of two circles is 16 : 9. Find the ratio between their :
(i) radius
(ii) diameters
(iii) circumference
The diameter of every wheel of a car is 63 cm. How much distance will the car move during the 2000 revolutions of its wheel.
The diameter of the wheel of a car is 70 cm. How many revolutions will it make to travel one kilometer?
The length and breadth of a rectangular paper are 35 cm and 22 cm. Find the area of the largest circle which can be cut out of this paper.
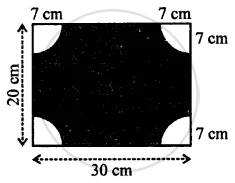
From each corner of a rectangular paper (30 cm x 20 cm) a quadrant of a circle of radius 7 cm is cut. Find the area of the remaining paper i.e., shaded portion.