Advertisements
Advertisements
Question
Find the area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2.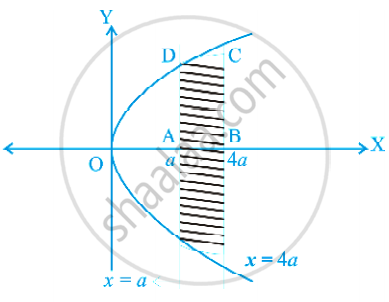
Solution
Given that x = at2 ......(i)
y = 2at ......(ii)
t = `y/(2"a")`
Putting the value of t in (i)
Wwe get y2 = 4ax
Putting t = 1 and t = 2 in (i)
We get x = a, and x = 4a
Required area = 2 area of ABCD
= `2 int_"a"^(4"a") y"d"x`
= `2 xx 2 int_"a"^(4"a") sqrt("a"x) "d"x`
= `8sqrt("a") |(x)^(3/2)/3|_"a"^(4"a")`
= `56/3 "a"^2` sq.units
APPEARS IN
RELATED QUESTIONS
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
Using integration finds the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).
Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
A. 2 (π – 2)
B. π – 2
C. 2π – 1
D. 2 (π + 2)
Area lying between the curve y2 = 4x and y = 2x is
A. 2/3
B. 1/3
C. 1/4
D. 3/4
Using the method of integration find the area bounded by the curve |x| + |y| = 1 .
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and
– x – y = 1].
Find the area bounded by curves {(x, y) : y ≥ x2 and y = |x|}.
Choose the correct answer The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
A. `4/3 (4pi - sqrt3)`
B. `4/3 (4pi + sqrt3)`
C. `4/3 (8pi - sqrt3)`
D.`4/3 (4pi + sqrt3)`
The area bounded by the y-axis, y = cos x and y = sin x when 0 <= x <= `pi/2`
(A) 2 ( 2 −1)
(B) `sqrt2 -1`
(C) `sqrt2 + 1`
D. `sqrt2`
Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0, 4) and (2, 3).
Solve the following :
Find the area of the region lying between the parabolas :
y2 = 4x and x2 = 4y
The area of the region included between the parabolas y2 = 16x and x2 = 16y, is given by ______ sq.units
The area of triangle ΔABC whose vertices are A(1, 1), B(2, 1) and C(3, 3) is ______ sq.units
Find the area of the ellipse `x^2/1 + y^2/4` = 1, in first quadrant
Find the area of the ellipse `x^2/36 + y^2/64` = 1, using integration
Find the area of the region lying between the parabolas 4y2 = 9x and 3x2 = 16y
Find the area enclosed between the circle x2 + y2 = 9, along X-axis and the line x = y, lying in the first quadrant
Find the area of the region included between the parabola y = `(3x^2)/4` and the line 3x – 2y + 12 = 0.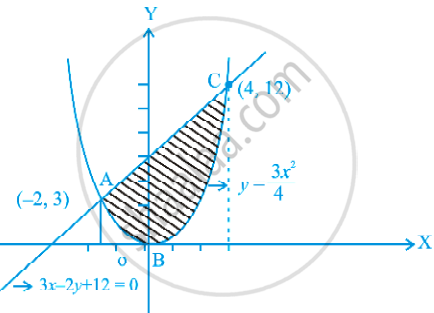
Calcualte the area under the curve y = `2sqrt(x)` included between the lines x = 0 and x = 1
Area lying between the curves `y^2 = 4x` and `y = 2x`
Using Integration, find the area of triangle whose vertices are (– 1, 1), (0, 5) and (3, 2).
Find the area enclosed between 3y = x2, X-axis and x = 2 to x = 3.
