Advertisements
Advertisements
Question
Find the area bounded by curves {(x, y) : y ≥ x2 and y = |x|}.
Solution
The area bounded by the curves, {(x, y) : y ≥ x2 and y = |x|}., is represented by the shaded region as
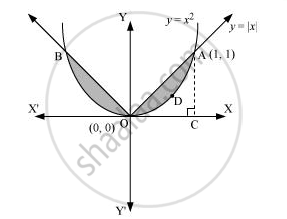
It can be observed that the required area is symmetrical about y-axis.
APPEARS IN
RELATED QUESTIONS
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region lying between the parabolas y2 = 4ax and x2 = 4ay.
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
A. 2 (π – 2)
B. π – 2
C. 2π – 1
D. 2 (π + 2)
Using the method of integration find the area bounded by the curve |x| + |y| = 1 .
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and
– x – y = 1].
Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0, 4) and (2, 3).
Area enclosed between the curve y2 (2a − x) = x3 and the line x = 2a above x-axis is ___________ .
Area lying between the curves y2 = 4x and y = 2x is
The area of the region included between the parabolas y2 = 16x and x2 = 16y, is given by ______ sq.units
The area enclosed between the two parabolas y2 = 20x and y = 2x is ______ sq.units
The area of triangle ΔABC whose vertices are A(1, 1), B(2, 1) and C(3, 3) is ______ sq.units
Find the area enclosed between y = cos x and X-axis between the lines x = `pi/2` and x ≤ `(3pi)/2`
Find the area of the ellipse `x^2/1 + y^2/4` = 1, in first quadrant
Find the area of sector bounded by the circle x2 + y2 = 25, in the first quadrant−
Find the area enclosed between the X-axis and the curve y = sin x for values of x between 0 to 2π
Find the area of the ellipse `x^2/36 + y^2/64` = 1, using integration
Find the area of the region included between y = x2 + 5 and the line y = x + 7
Find the area enclosed between the circle x2 + y2 = 9, along X-axis and the line x = y, lying in the first quadrant
Find the area enclosed by the curve x = 3 cost, y = 2 sint.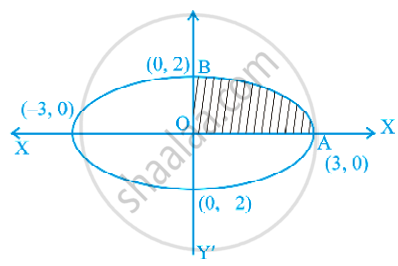
Find the area of the region included between the parabola y = `(3x^2)/4` and the line 3x – 2y + 12 = 0.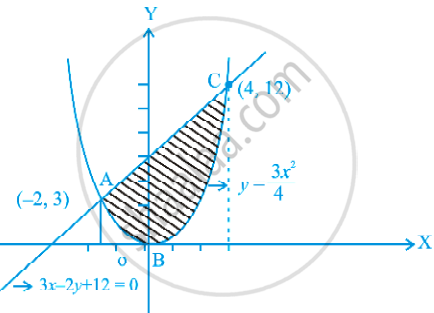
Find the area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2.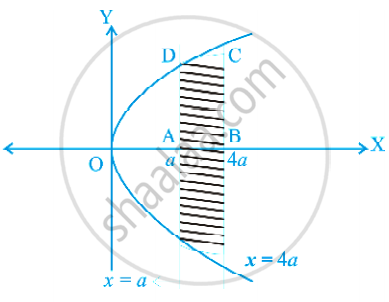
Find the area of a minor segment of the circle x2 + y2 = a2 cut off by the line x = `"a"/2`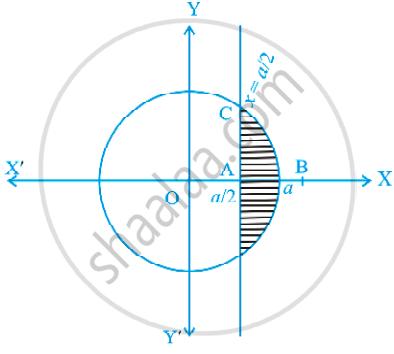
Calcualte the area under the curve y = `2sqrt(x)` included between the lines x = 0 and x = 1
Determine the area under the curve y = `sqrt("a"^2 - x^2)` included between the lines x = 0 and x = a.
Area lying between the curves `y^2 = 4x` and `y = 2x`
The value of a for which the area between the curves y2 = 4ax and x2 = 4ay is 1 sq.unit, is ______.
Using Integration, find the area of triangle whose vertices are (– 1, 1), (0, 5) and (3, 2).
Find the area cut off from the parabola 4y = 3x2 by the line 2y = 3x + 12.
