Advertisements
Advertisements
Question
Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0, 4) and (2, 3).
Solution
Let the vertices of the triangle be A(–2, 1), B(0, 4) and C(2, 3).
Equation of line segment AB is
`(y - 1) = (4-1)/(0+2) (x + 2)`
`=>y = (3(x + 2))/2 + 1`
`=> y = (3x + 6 + 2)/2`
`=> y = (3x + 8)/2`
Equation of line segment BC is
`(y - 4) = (3-4)/(2 - 0) (x - 0)`
`=> y = -1/2x + 4`
Equation of line segment AC is
`(y - 3) = (1-3)/(-2-2) (x - 2)`
`=> y = 1/2(x - 2) + 3`
`=> y = x/2 - 1 + 3`
`=> y = x/2 + 2`
The graph of the given equations is shown below:
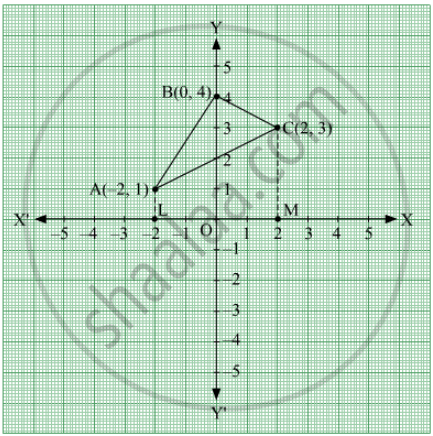
AL, BO and CM are drawn perpendicular to x-axis.
It can be observed in the following figure that,
Area (ΔACB) = Area (ABOL) + Area (BOMCB) – Area (ALMCA) ….. (1)

Required area = Area (ΔACB) = Area (ABOL) + Area (BOMCB) – Area (ALMCA)
= 5 + 7 − 8
= 4 sq units
APPEARS IN
RELATED QUESTIONS
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the region lying between the parabolas y2 = 4ax and x2 = 4ay.
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y 2 = 1
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
Using integration finds the area of the region bounded by the triangle whose vertices are (–1, 0), (1, 3) and (3, 2).
Using integration find the area of the triangular region whose sides have the equations y = 2x +1, y = 3x + 1 and x = 4.
Using the method of integration find the area bounded by the curve |x| + |y| = 1 .
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and
– x – y = 1].
Find the area bounded by curves {(x, y) : y ≥ x2 and y = |x|}.
Choose the correct answer The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
A. `4/3 (4pi - sqrt3)`
B. `4/3 (4pi + sqrt3)`
C. `4/3 (8pi - sqrt3)`
D.`4/3 (4pi + sqrt3)`
The area bounded by the y-axis, y = cos x and y = sin x when 0 <= x <= `pi/2`
(A) 2 ( 2 −1)
(B) `sqrt2 -1`
(C) `sqrt2 + 1`
D. `sqrt2`
Find the area included between the parabolas y2 = 4ax and x2 = 4by.
Area enclosed between the curve y2 (2a − x) = x3 and the line x = 2a above x-axis is ___________ .
Solve the following :
Find the area of the region lying between the parabolas :
y2 = 4x and x2 = 4y
The area enclosed between the two parabolas y2 = 20x and y = 2x is ______ sq.units
Find the area enclosed between y = cos x and X-axis between the lines x = `pi/2` and x ≤ `(3pi)/2`
Find the area of sector bounded by the circle x2 + y2 = 25, in the first quadrant−
Find the area of the region lying between the parabolas 4y2 = 9x and 3x2 = 16y
Find the area of the region included between y = x2 + 5 and the line y = x + 7
Find the area enclosed by the curve x = 3 cost, y = 2 sint.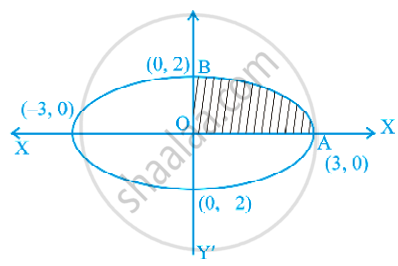
Find the area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2.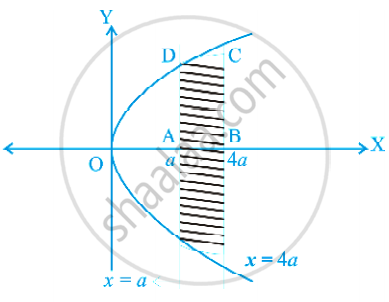
Find the area of a minor segment of the circle x2 + y2 = a2 cut off by the line x = `"a"/2`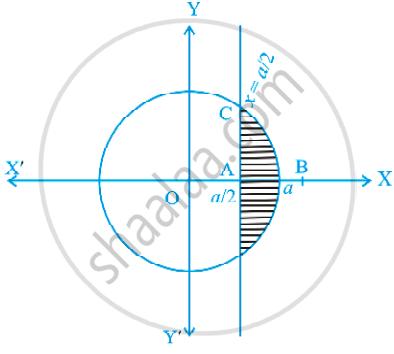
Determine the area under the curve y = `sqrt("a"^2 - x^2)` included between the lines x = 0 and x = a.
Area lying between the curves `y^2 = 4x` and `y = 2x`
The value of a for which the area between the curves y2 = 4ax and x2 = 4ay is 1 sq.unit, is ______.
Using Integration, find the area of triangle whose vertices are (– 1, 1), (0, 5) and (3, 2).
