Advertisements
Advertisements
Question
Area enclosed between the curve y2 (2a − x) = x3 and the line x = 2a above x-axis is ___________ .
Options
πa2
\[\frac{3}{2}\pi a^2\]
2πa2
3πa2
Solution
\[\frac{3}{2}\pi a^2\]
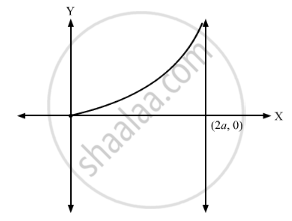
\[\begin{array}{l}y^2 \left( 2a -x \right) = x^3 \\ y = \sqrt{\frac{x^3}{2a - x}}\end{array}\]
Let x = 2a sin2θ
dx = 4a sinθ cosθ dθ
\[\begin{array}{l}\text{ Area }= \hspace{0.167em} \int\limits_0^{2a} \sqrt{\frac{x^3}{2a - x}}dx \\ = \int_0^\frac{\pi}{2} \sqrt{\frac{\left( 8 a^3 \right) \sin^6 \theta}{\left( 2a \right)\hspace{0.167em} \cos^2 \theta}}\hspace{0.167em} \cdot \left( 4a \right)\hspace{0.167em}\sin\theta\hspace{0.167em}\cos\theta\hspace{0.167em}d\theta \\ = 8 a^2 \int_0^\frac{\pi}{2} \sqrt{\sin^6 \theta}\hspace{0.167em}\sin\theta\hspace{0.167em}d\theta \\ = 8 a^2 \left[ \int_0^\frac{\pi}{2} \sin^4 \theta\hspace{0.167em}d\theta \right] \\ = 8 a^2 \left[ \int_0^\frac{\pi}{2} \sin^2 \theta\left( 1- \cos^2 \theta \right)\hspace{0.167em}d\theta \right] \\ = 8 a^2 \left[ \int_0^\frac{\pi}{2} \left( \frac{1 - \cos2\theta}{2} \right) d\theta - \frac{1}{4} \int_0^\frac{\pi}{2} \sin^2 2\theta \text{ d}\theta \right] \\ = 8 a^2 \left[ \frac{1}{2} \left[ \theta \right]_0^\frac{\pi}{2} - \left[ \frac{\sin2\theta}{4} \right]_0^\frac{\pi}{2} \right] - \frac{1}{4}\left[ \int_0^\frac{\pi}{2} \frac{1 - \cos 4\theta}{2}d\theta \right] \\ = 8 a^2 \left[ \left( \frac{\pi}{4} \right) - 0 \right] - \frac{1}{4}\left[ \frac{\pi}{4} - 0 \right] \\ = 8 a^2 \left[ \frac{\pi}{4} - \frac{\pi}{16} \right] = \frac{3}{2}\pi a^2\end{array}\]
APPEARS IN
RELATED QUESTIONS
Using integration, find the area of the region bounded by the triangle whose vertices are (−1, 2), (1, 5) and (3, 4).
Find the area of the circle 4x2 + 4y2 = 9 which is interior to the parabola x2 = 4y
Find the area bounded by curves (x – 1)2 + y2 = 1 and x2 + y 2 = 1
Find the area of the region bounded by the curves y = x2 + 2, y = x, x = 0 and x = 3
Smaller area enclosed by the circle x2 + y2 = 4 and the line x + y = 2 is
A. 2 (π – 2)
B. π – 2
C. 2π – 1
D. 2 (π + 2)
Area lying between the curve y2 = 4x and y = 2x is
A. 2/3
B. 1/3
C. 1/4
D. 3/4
Using the method of integration find the area bounded by the curve |x| + |y| = 1 .
[Hint: The required region is bounded by lines x + y = 1, x– y = 1, – x + y = 1 and
– x – y = 1].
Choose the correct answer The area of the circle x2 + y2 = 16 exterior to the parabola y2 = 6x is
A. `4/3 (4pi - sqrt3)`
B. `4/3 (4pi + sqrt3)`
C. `4/3 (8pi - sqrt3)`
D.`4/3 (4pi + sqrt3)`
The area bounded by the y-axis, y = cos x and y = sin x when 0 <= x <= `pi/2`
(A) 2 ( 2 −1)
(B) `sqrt2 -1`
(C) `sqrt2 + 1`
D. `sqrt2`
Using integration, find the area of region bounded by the triangle whose vertices are (–2, 1), (0, 4) and (2, 3).
Show that the rectangle of the maximum perimeter which can be inscribed in the circle of radius 10 cm is a square of side `10sqrt2` cm.
Find the area included between the parabolas y2 = 4ax and x2 = 4by.
The area enclosed between the curves y = loge (x + e), x = loge \[\left( \frac{1}{y} \right)\] and the x-axis is _______ .
The area between x-axis and curve y = cos x when 0 ≤ x ≤ 2 π is ___________ .
Area lying between the curves y2 = 4x and y = 2x is
Solve the following :
Find the area of the region lying between the parabolas :
y2 = 4x and x2 = 4y
The area of the region included between the parabolas y2 = 16x and x2 = 16y, is given by ______ sq.units
Find the area enclosed between y = cos x and X-axis between the lines x = `pi/2` and x ≤ `(3pi)/2`
Find the area of the ellipse `x^2/1 + y^2/4` = 1, in first quadrant
Find the area of sector bounded by the circle x2 + y2 = 25, in the first quadrant−
Find the area of the ellipse `x^2/36 + y^2/64` = 1, using integration
Find the area of the region lying between the parabolas 4y2 = 9x and 3x2 = 16y
Find the area enclosed between the circle x2 + y2 = 9, along X-axis and the line x = y, lying in the first quadrant
Find the area of the region bounded by the curves x = at2 and y = 2at between the ordinate corresponding to t = 1 and t = 2.
Find the area of a minor segment of the circle x2 + y2 = a2 cut off by the line x = `"a"/2`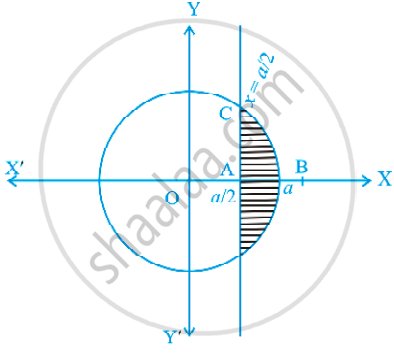
Calcualte the area under the curve y = `2sqrt(x)` included between the lines x = 0 and x = 1
Determine the area under the curve y = `sqrt("a"^2 - x^2)` included between the lines x = 0 and x = a.
Area lying between the curves `y^2 = 4x` and `y = 2x`
The value of a for which the area between the curves y2 = 4ax and x2 = 4ay is 1 sq.unit, is ______.
Find the area enclosed between 3y = x2, X-axis and x = 2 to x = 3.
Find the area cut off from the parabola 4y = 3x2 by the line 2y = 3x + 12.
