Advertisements
Advertisements
Question
Find the equation of the circle on the line joining the points (1, 0), (0, 1), and having its centre on the line x + y = 1.
Solution
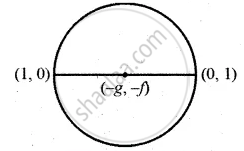
Let the equation of the circle be
x2 + y2 + 2gx + 2fy + c = 0 ……… (1)
The circle passes through (1, 0)
12 + 02 + 2g(1) + 2f(0) + c = 0
1 + 2g + c = 0
2g + c = 1 …….. (2)
Again the circle (1) passes through (0, 1)
02 + 12 + 2g(0) + 2f(1) + c = 0
1 + 2f + c = 0
2f + c = -1 ……. (3)
(2) – (3) gives 2g – 2f = 0 (or) g – f = 0 ………. (4)
Given that the centre of the circle (-g, -f) lies on the line x + y = 1
-g – f = 1 …….. (5)
(4) + (5) gives -2f = 1 ⇒ f = `- 1/2`
Using f = `- 1/2` in (5) we get
- g - `(- 1/2)` = 1
- g = `1 - (- 1/2) = 1/2`
g = `- 1/2`
Using g = `- 1/2` in (2) we get
`2(- 1/2) + "c" = - 1`
-1 + c = -1
c = 0
using g = `-1/2`, f = `-1/2`, c = 0 in (1) we get the equation of the circle,
`x^2 + y^2 + 2(- 1/2)x + 2(- 1/2)y + 0 = 0`
x2 + y2 – x – y = 0
APPEARS IN
RELATED QUESTIONS
Find the equation of the following circles having the centre (3, 5) and radius 5 units.
Find the equation of the circle whose centre is (-3, -2) and having circumference 16π.
Find the Cartesian equation of the circle whose parametric equations are x = 3 cos θ, y = 3 sin θ, 0 ≤ θ ≤ 2π.
Find the length of the tangent from (1, 2) to the circle x2 + y2 – 2x + 4y + 9 = 0.
Find the value of P if the line 3x + 4y – P = 0 is a tangent to the circle x2 + y2 = 16.
The length of the tangent from (4, 5) to the circle x2 + y2 = 16 is:
If the centre of the circle is (-a, -b) and radius is `sqrt("a"^2 - "b"^2)` then the equation of circle is:
Find the equation of circles that touch both the axes and pass through (− 4, −2) in general form
A circle of area 9π square units has two of its diameters along the lines x + y = 5 and x – y = 1. Find the equation of the circle
Find centre and radius of the following circles
x2 + y2 – x + 2y – 3 = 0
