Advertisements
Advertisements
Question
Find the equation of the circle whose centre is (2, 3) and which passes through (1, 4).
Solution
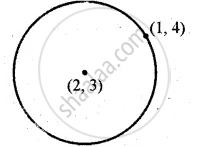
Centre (h, k) = (2, 3)
Radius = `sqrt((1 - 2)^2 + (4 - 3)^2)`
`= sqrt((-1)^2 + 1^2)`
`= sqrt2`
Equation of the circle with centre (h, k) and radius r is (x – h)2 + (y – k)2 = r2
⇒ (x – 2)2 + (y – 3)2 = `(sqrt2)^2`
⇒ x2 – 4x + 4 + y2 – 6y + 9 = 2
⇒ x2 + y2 – 4x – 6y + 11 = 0
APPEARS IN
RELATED QUESTIONS
Find the equation of the following circles having the centre (3, 5) and radius 5 units.
Find the centre and radius of the circle.
5x2 + 5y2+ 4x – 8y – 16 = 0
Find the equation of the circle on the line joining the points (1, 0), (0, 1), and having its centre on the line x + y = 1.
The equation of the circle with centre on the x axis and passing through the origin is:
Find the equation of the circles with centre (2, 3) and passing through the intersection of the lines 3x – 2y – 1 = 0 and 4x + y – 27 = 0
Determine whether the points (– 2, 1), (0, 0) and (– 4, – 3) lie outside, on or inside the circle x2 + y2 – 5x + 2y – 5 = 0
Find centre and radius of the following circles
x2 + y2 + 6x – 4y + 4 = 0
Choose the correct alternative:
If the normals of the parabola y2 = 4x drawn at the end points of its latus rectum are tangents to the circle (x – 3)2 + (y + 2)2 = r2, then the value of r2 is
Choose the correct alternative:
The circle passing through (1, – 2) and touching the axis of x at (3, 0) passing through the point
Choose the correct alternative:
If the coordinates at one end of a diameter of the circle x2 + y2 – 8x – 4y + c = 0 are (11, 2) the coordinates of the other end are
