Advertisements
Advertisements
Question
Find the zeroes of the following polynomials by factorisation method and verify the relations between the zeroes and the coefficients of the polynomials:
5t2 + 12t + 7
Solution
5t2 + 12t + 7
Splitting the middle term, we get,
5t2 + 5t + 7t + 7
Taking the common factors out, we get,
5t(t + 1) + 7(t + 1)
On grouping, we get,
(t + 1)(5t + 7)
So, the zeroes are,
t + 1 = 0
`\implies` y = –1
5t + 7 = 0
`\implies` 5t = –7
`\implies` t = `-7/5`
Therefore, zeroes are `(-7/5)` and –1
Verification:
Sum of the zeroes = – (coefficient of x) ÷ coefficient of x2
α + β = `- b/a`
`(-1) + (-7/5) = - (12)/5`
= `-12/5 = -12/5`
Product of the zeroes = constant term ÷ coefficient of x2
αβ = `c/a`
`(-1)(-7/5) = 7/5`
`7/5 = 7/5`
APPEARS IN
RELATED QUESTIONS
Find the zeroes of the following quadratic polynomial and verify the relationship between the zeroes and the coefficients:
3x2 – x – 4
Find a quadratic polynomial each with the given numbers as the sum and product of its zeroes respectively.
`1/4 , -1`
Find a quadratic polynomial with the given numbers as the sum and product of its zeroes respectively.
`0, sqrt5`
If α and β are the zeros of the quadratic polynomial f(x) = ax2 + bx + c, then evaluate :
`a(α^2/β+β^2/α)+b(α/β+β/α)`
If α and β are the zeros of the quadratic polynomial p(y) = 5y2 − 7y + 1, find the value of `1/alpha+1/beta`
If If α and β are the zeros of the quadratic polynomial f(x) = x2 – 2x + 3, find a polynomial whose roots are α + 2, β + 2.
Define a polynomial with real coefficients.
Basketball and soccer are played with a spherical ball. Even though an athlete dribbles the ball in both sports, a basketball player uses his hands and a soccer player uses his feet. Usually, soccer is played outdoors on a large field and basketball is played indoor on a court made out of wood. The projectile (path traced) of soccer ball and basketball are in the form of parabola representing quadratic polynomial.

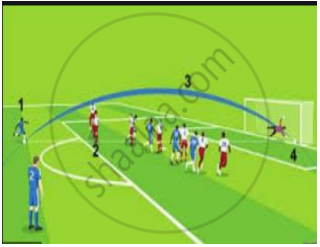
What will be the expression of the polynomial?
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is ______.
Find the zeroes of the quadratic polynomial 4s2 – 4s + 1 and verify the relationship between the zeroes and the coefficients.
