Advertisements
Advertisements
Question
For an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using the expression w = `- nRT` In `V_f/V_i`. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversibly to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively.
(i) Work done at 600 K is 20 times the work done at 300 K.
(ii) Work done at 300 K is twice the work done at 600 K.
(iii) Work done at 600 K is twice the work done at 300 K.
(iv) ∆U = 0 in both cases.
Solution
(iii) Work done at 600 K is twice the work done at 300 K.
(iv) ∆U = 0 in both cases.
Explanation:
For isothermal reversible change, we know
q = – w = `nRT` In `V_f/V_i` = 2.303 `nRT` log `V_f/V_i`
`(W_(600 K))/(W_(300 K)) = (1 xx R xx 600 K In 1/10)/(1 xx R xx 300 K In 1/10) = 600/300` = 2
For isothermal expansion of ideal gases, ΔU = 0.
Since temperature is constant this means there is no change in internal energy.
APPEARS IN
RELATED QUESTIONS
The pressure-volume work for an ideal gas can be calculated by using the expression w = `- int_(v_i)^(v_f) p_(ex) dV`. The work can also be calculated from the pV– plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from volume Vi to Vf. choose the correct option.
What will be the work done on an ideal gas enclosed in a cylinder, when it is compressed by a constant external pressure, pext in a single step as shown in figure. Explain graphically.
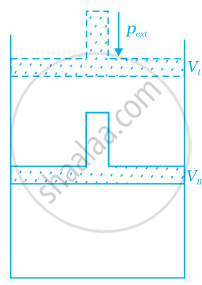
How will you calculate work done on an ideal gas in a compression, when change in pressure is carried out in infinite steps?
Represent the potential energy/enthalpy change in the following processes graphically.
(a) Throwing a stone from the ground to roof.
(b) \[\ce{1/2 H2(g) + 1/2 Cl2 (g) ⇌ HCl (g) Δ_rH^Θ = - 92.32 kJ mol^{-1}}\]
In which of the processes potential energy/enthalpy change is contributing factor to the spontaneity?
1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.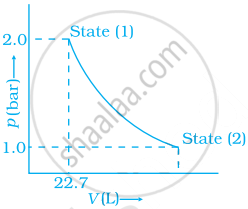
Match the following :
| Column I | Column II |
| (i) Entropy of vapourisation | (a) decreases |
| (ii) K for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) ∆U in adiabatic expansion of ideal gas | (d) `(∆H_(vap))/T_b` |
Graphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from \[\ce{(p_i, V_i)}\] to \[\ce{(p_f , V_f )}\]. With the help of a pV plot compare the work done in the above case with that carried out against a constant external pressure \[\ce{p_f}\].
For silver Cp (J K-1 mol-1) = 23 + 0.01 T. If the temperature (T) of 3 moles of silver is raised from 300 K to 1000 K at 1 atom pressure, the value of ΔH will be close to ______.
Calculate the work involved when 1 mol of an ideal gas is compressed reversibly from 1.00 bar to 5.00 bar at a constant temperature of 300 K ______.
1 mole of an ideal monoatomic gas initially at 1 atm and 300 K experiences a process by which pressure is doubled. The nature of the process is unspecified but 6. ΔU = 900 cal. The final volume will be ______ l.
[Given : R = 0.08 atm lit. I mol/K = 2 Cal/K/mol J]
