Advertisements
Advertisements
Question
Match the following :
| Column I | Column II |
| (i) Entropy of vapourisation | (a) decreases |
| (ii) K for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) ∆U in adiabatic expansion of ideal gas | (d) `(∆H_(vap))/T_b` |
Solution
| Column I | Column II |
| (i) Entropy of vapourisation | (d) `(∆H_(vap))/T_b` |
| (ii) K for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) ∆U in adiabatic expansion of ideal gas | (a) decreases |
APPEARS IN
RELATED QUESTIONS
For an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using the expression w = `- nRT` In `V_f/V_i`. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversibly to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively.
(i) Work done at 600 K is 20 times the work done at 300 K.
(ii) Work done at 300 K is twice the work done at 600 K.
(iii) Work done at 600 K is twice the work done at 300 K.
(iv) ∆U = 0 in both cases.
A sample of 1.0 mol of a monoatomic ideal gas is taken through a cyclic process of expansion and compression as shown in figure 6.1. What will be the value of ∆H for the cycle as a whole?

Expansion of a gas in vacuum is called free expansion. Calculate the work done and the change in internal energy when 1 litre of ideal gas expands isothermally into vacuum until its total volume is 5 litre?
1.0 mol of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in figure. Calculate the work done for the expansion of gas from state (1) to state (2) at 298 K.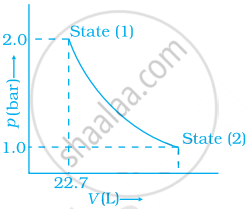
An ideal gas is allowed to expand against a constant pressure of 2 bar from 10 L to 50 L in one step. Calculate the amount of work done by the gas. If the same expansion were carried out reversibly, will the work done be higher or lower than the earlier case? (Given that 1 L bar = 100 J)
Match the following :
| A | B |
| (i) Adiabatic process | (a) Heat |
| (ii) Isolated system | (b) At constant volume |
| (iii) Isothermal change | (c) First law of thermodynamics |
| (iv) Path function | (d) No exchange of energy and matter |
| (v) State function | (e) No transfer of heat |
| (vi) ΔU = q | (f) Constant temperature |
| (vii) Law of conservation of energy | (g) Internal energy |
| (viii) Reversible process | (h) Pext = o |
| (ix) Free expansion | (i) At constant pressure |
| (x) ΔH = q | (j) Infinitely slow process which proceeds through a series of equilibrium states. |
| (xi) Intensive property | (k) Entropy |
| (xii) Extensive property | (l) Pressure |
| (m) Specific heat |
Graphically show the total work done in an expansion when the state of an ideal gas is changed reversibly and isothermally from \[\ce{(p_i, V_i)}\] to \[\ce{(p_f , V_f )}\]. With the help of a pV plot compare the work done in the above case with that carried out against a constant external pressure \[\ce{p_f}\].
Calculate the work involved when 1 mol of an ideal gas is compressed reversibly from 1.00 bar to 5.00 bar at a constant temperature of 300 K ______.
1 mole of an ideal monoatomic gas initially at 1 atm and 300 K experiences a process by which pressure is doubled. The nature of the process is unspecified but 6. ΔU = 900 cal. The final volume will be ______ l.
[Given : R = 0.08 atm lit. I mol/K = 2 Cal/K/mol J]
1 mole of an ideal monoatomic gas initially at 1 atm and 300 K experiences a process by which pressure is doubled. The nature of the process is unspecified but 6. ΔU = 900 cal. The final volume will be ______ l.
[Given : R = 0.08 atm lit. I mol/K = 2 Cal/K/mol J]
