Advertisements
Advertisements
प्रश्न
Match the following :
| Column I | Column II |
| (i) Entropy of vapourisation | (a) decreases |
| (ii) K for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) ∆U in adiabatic expansion of ideal gas | (d) `(∆H_(vap))/T_b` |
उत्तर
| Column I | Column II |
| (i) Entropy of vapourisation | (d) `(∆H_(vap))/T_b` |
| (ii) K for spontaneous process | (b) is always positive |
| (iii) Crystalline solid state | (c) lowest entropy |
| (iv) ∆U in adiabatic expansion of ideal gas | (a) decreases |
APPEARS IN
संबंधित प्रश्न
The pressure-volume work for an ideal gas can be calculated by using the expression w = `- int_(v_i)^(v_f) p_(ex) dV`. The work can also be calculated from the pV– plot by using the area under the curve within the specified limits. When an ideal gas is compressed (a) reversibly or (b) irreversibly from volume Vi to Vf. choose the correct option.
For an ideal gas, the work of reversible expansion under isothermal condition can be calculated by using the expression w = `- nRT` In `V_f/V_i`. A sample containing 1.0 mol of an ideal gas is expanded isothermally and reversibly to ten times of its original volume, in two separate experiments. The expansion is carried out at 300 K and at 600 K respectively.
(i) Work done at 600 K is 20 times the work done at 300 K.
(ii) Work done at 300 K is twice the work done at 600 K.
(iii) Work done at 600 K is twice the work done at 300 K.
(iv) ∆U = 0 in both cases.
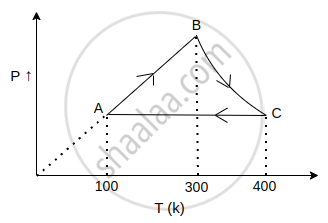
A sample of 1.0 mol of a monoatomic ideal gas is taken through a cyclic process of expansion and compression as shown in figure 6.1. What will be the value of ∆H for the cycle as a whole?

Expansion of a gas in vacuum is called free expansion. Calculate the work done and the change in internal energy when 1 litre of ideal gas expands isothermally into vacuum until its total volume is 5 litre?
Match the following :
| A | B |
| (i) Adiabatic process | (a) Heat |
| (ii) Isolated system | (b) At constant volume |
| (iii) Isothermal change | (c) First law of thermodynamics |
| (iv) Path function | (d) No exchange of energy and matter |
| (v) State function | (e) No transfer of heat |
| (vi) ΔU = q | (f) Constant temperature |
| (vii) Law of conservation of energy | (g) Internal energy |
| (viii) Reversible process | (h) Pext = o |
| (ix) Free expansion | (i) At constant pressure |
| (x) ΔH = q | (j) Infinitely slow process which proceeds through a series of equilibrium states. |
| (xi) Intensive property | (k) Entropy |
| (xii) Extensive property | (l) Pressure |
| (m) Specific heat |
The net work done in the following cycle for one mol of an ideal gas will be ______ (in calorie), where in process BC, PT = constant. (R = 2 cal/mol-K).
1 mole of an ideal monoatomic gas initially at 1 atm and 300 K experiences a process by which pressure is doubled. The nature of the process is unspecified but 6. ΔU = 900 cal. The final volume will be ______ l.
[Given : R = 0.08 atm lit. I mol/K = 2 Cal/K/mol J]
1 mole of an ideal monoatomic gas initially at 1 atm and 300 K experiences a process by which pressure is doubled. The nature of the process is unspecified but 6. ΔU = 900 cal. The final volume will be ______ l.
[Given : R = 0.08 atm lit. I mol/K = 2 Cal/K/mol J]
Find the work done when 2 moles of hydrogen expand isothermally from 15 to 50 litres against a constant pressure of 1 atm at 25°C.
Five moles of an ideal gas at 1 bar and 298 K is expanded into the vacuum to double the volume. The work done is ______.
