Advertisements
Advertisements
Question
If α and β are the zeroes of the polynomial x2 – 1, then the value of (α + β) is ______.
Options
2
1
–1
0
Solution
If α and β are the zeroes of the polynomial x2 – 1, then the value of (α + β) is 0.
Explanation:
Sum of zeroes of the quadratic equation
ax2 + bx + c = 0 is `(-b)/a`
∴ Sum of zeroes of x2 – 1 = x2 + 0x – 1 = 0 is `(-0)/1` = 0
∴ α + β = 0
APPEARS IN
RELATED QUESTIONS
Find all the zeroes of `(2x^4 – 3x^3 – 5x2 + 9x – 3)`, it is being given that two of its zeroes are `sqrt3 and –sqrt3`.
If -4 is a zero of the polynomial `x^2 – x – (2k + 2) is –4`, then find the value of k.
If -2 is a zero of the polynomial `3x^2 + 4x + 2k` then find the value of k.
If 𝛼, 𝛽 are the zeroes of the polynomial `f(x) = x^2 – 5x + k` such that 𝛼 - 𝛽 = 1, find the value of k = ?
Find the value of k such that the polynomial x2-(k +6)x+ 2(2k - 1) has some of its zeros equal to half of their product.
The number of polynomials having zeroes as -2 and 5 is ______.
Given that one of the zeroes of the cubic polynomial ax3 + bx2 + cx + d is zero, the product of the other two zeroes is ______.
The zeroes of the quadratic polynomial x2 + 99x + 127 are ______.
Which of the following is not the graph of a quadratic polynomial?
The graph of y = f(x) is shown in the figure for some polynomial f(x).
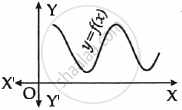
The number of zeroes of f(x) is ______.
