Advertisements
Advertisements
Question
If I toss a coin 3 times and get head each time, should I expect a tail to have a higher chance in the 4th toss? Give reason in support of your answer.
Solution
No, let we toss a coin, then we get head or tail, both are equally likely events i.e., probability of each event is `1/2`.
So, no question of expecting a tail to have a higher chance in 4th toss.
APPEARS IN
RELATED QUESTIONS
In a simultaneous throw of a pair of dice, find the probability of getting a sum less than 6
A bag contains 4 red, 5 black and 6 white balls. A ball is drawn from the bag at random. Find the probability that the ball drawn is Red
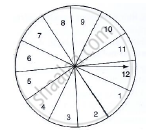
A game of chance consists of spinning an arrow which is equally likely to come to rest
pointing to one of the number, 1, 2, 3, ..., 12 as shown in Fig. below. What is the
probability that it will point to an even number?
It is given that m a group of 3 students, the probability of 2 students not having the same birthday is 0.992. What is the probability that the 2 students have the same birthday?
A box contains loo red cards, 200 yellow cards and 50 blue cards. If a card is drawn at random from the box, then find the probability that it will be a blue card
A game consists of spinning an arrow which comes to rest pointing at one of the numbers 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12; as shown below.
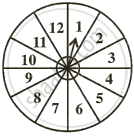
If the outcomes are equally likely, find the probability that the pointer will point at:
- 6
- an even number.
- a prime number.
- a number greater than 8.
- a number less than or equal to 9.
- a number between 3 and 11.
Offices in Delhi are open for five days in a week (Monday to Friday). Two employees of an office remain absent for one day in the same particular week. Find the probability that they remain absent on different days.
In a game, the entry fee is Rs 5. The game consists of a tossing a coin 3 times. If one or two heads show, Sweta gets her entry fee back. If she throws 3 heads, she receives double the entry fees. Otherwise she will lose. For tossing a coin three times, find the probability that she gets double entry fee.
Assertion (A): The probability that a leap year has 53 Sundays is `2/7`.
Reason (R): The probability that a non-leap year has 53 Sundays is `1/2`.
The following letters A, D, M, N, O, S, U, Y of the English alphabet are written on separate cards and put in a box. The cards are well shuffled and one card is drawn at random. What is the probability that the card drawn is a letter of the word,
- MONDAY?
- Which does not appear in MONDAY?
- Which appears both in SUNDAY and MONDAY?
