Advertisements
Advertisements
Question
If in ΔABC, `vec(BA) = 2veca` and `vec(BC) = 3vecb`, then `vec(AC)` is ______.
Options
`2veca + 3vecb`
`2veca - 3vecb`
`3vecb - 2veca`
`-2veca - 3vecb`
Solution
If in ΔABC, `vec(BA) = 2veca` and `vec(BC) = 3vecb`, then `vec(AC)` is `underlinebb(3vecb - 2veca)`.
Explanation:
By triangle law of vector addition,
`vec(AC) = vec(AB) + vec(BC)`
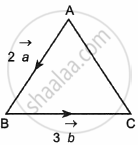
`vec(AC) = -vec(BA) + vec(BC)`
= `-2veca + 3vecb`
= `3vecb - 2veca`
APPEARS IN
RELATED QUESTIONS
Find the values of x and y so that the vectors `2hati + 3hatj and xhati + yhatj` are equal.
Find the scalar and vector components of the vector with initial point (2, 1) and terminal point (–5, 7).
Find the sum of the vectors `veca = hati -2hatj + hatk, vecb = -2hati + 4hatj + 5hatk and vecc = hati - 6hatj - 7hatk.`
In triangle ABC, which of the following is not true:

If `veca` and `vecb` are two collinear vectors, then which of the following are incorrect:
A girl walks 4 km towards west, then she walks 3 km in a direction 30° east of north and stops. Determine the girl’s displacement from her initial point of departure.
If `veca = vecb + vecc`, then is it true that `|veca| = |vecb| + |vecc|`? Justify your answer.
The two adjacent sides of a parallelogram are `2hati - 4hatj + 5hatk` and `hati - 2hatj - 3hatk`. Find the unit vector parallel to its diagonal. Also, find its area.
Let `veca = hati + 4hatj + 2hatk, vecb = 3hati - 2hatj + 7hatk ` and `vecc = 2hati - hatj + 4hatk`. Find a vector `vecd` which is perpendicular to both `veca` and `vecb`, and `vecc.vecd = 15`.
ABCD is a quadrilateral. Find the sum the vectors \[\overrightarrow{BA} , \overrightarrow{BC} , \overrightarrow{CD}\] and \[\overrightarrow{DA}\]
Prove that the sum of all vectors drawn from the centre of a regular octagon to its vertices is the zero vector.
If P is a point and ABCD is a quadrilateral and \[\overrightarrow{AP} + \overrightarrow{PB} + \overrightarrow{PD} = \overrightarrow{PC}\], show that ABCD is a parallelogram.
ABCD is a parallelogram and P is the point of intersection of its diagonals. If O is the origin of reference, show that
\[\vec{OA} + \vec{OB} + \vec{OC} + \vec{OD} = 4 \vec{OP}\]
ABCD are four points in a plane and Q is the point of intersection of the lines joining the mid-points of AB and CD; BC and AD. Show that\[\vec{PA} + \vec{PB} + \vec{PC} + \vec{PD} = 4 \vec{PQ}\], where P is any point.
Write \[\overrightarrow{PQ} + \overrightarrow{RP} + \overrightarrow{QR}\] in the simplified form.
Find the sum of the following vectors: \[\overrightarrow{a} = \hat{i} - 2 \hat{j} , \overrightarrow{b} = 2 \hat{i} - 3 \hat{j} , \overrightarrow{c} = 2 \hat{i} + 3 \hat{k} .\]
Find the unit vector in the direction of the sum of the vectors `2hati + 3hatj - hatk and 4hati - 3hatj + 2hatk .`
Show that the sum of three vectors determined by the medians of a triangle directed from the vertices is zero.
If `6hati + 10hatj + 3hatk = x(hati + 3hatj + 5hatk) + y(hati - hatj + 5hatk) + z(hati + 3hatj - 4hatk)`, then ______
`[(bar"a", bar"b" + bar"c", bar"a" + bar"b" + bar"c")]` = ______.
`veca, vecb` and `vecc` are perpendicular to `vecb + vecc, vecc + veca` and `veca + vecb` respectively and if `|veca + vecb|` = 6, `|vecb + vecc|` = 8 and `|vecc + veca|` = 10, then `|veca + vecb + vecc|` is equal to
A vector whose initial and terminal point continues is known as:-
Find the value of `x` and `y`. so that the vectors `2hatj + 3hatj` and `xhati + yhati` are equal
ABCD is a rhombus whose diagonals intersect at E . Then `vec(EA) + vec(EB) + vec(EC) + vec(ED)` equals to ______.
