Advertisements
Advertisements
Question
If mercury and glass had equal coefficients of volume expansion, could we make a mercury thermometer in a glass tube?
Solution
Yes, we can make a mercury thermometer in a glass tube. Mercury and glass have equal coefficients of volume expansion. So, when temperature changes, the increase in the volume of the glass tube as which is equal to the real increase in volume minus the increase in the volume of the container, would be zero. Hence, it will give correct reading at every temperature.
APPEARS IN
RELATED QUESTIONS
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10–5 K–1.
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1, steel = 1.2 × 10–5 K–1).
If two bodies are in thermal equilibrium in one frame, will they be in thermal equilibrium in all frames?
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
For a constant-volume gas thermometer, one should fill the gas at
Answer the following question.
State applications of thermal expansion.
A glass flask has a volume 1 × 10−4 m3. It is filled with a liquid at 30°C. If the temperature of the system is raised to 100°C, how much of the liquid will overflow? (Coefficient of volume expansion of glass is 1.2 × 10−5 (°C)−1 while that of the liquid is 75 × 10−5 (°C)−1).
Solve the following problem.
In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 °C. If maximum temperature in the region is 45 °C and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10–5K–1 for the material of the rail section?
A bimetallic strip is made of aluminium and steel (αAl > αsteel) . On heating, the strip will ______.
Calculate the stress developed inside a tooth cavity filled with copper when hot tea at temperature of 57°C is drunk. You can take body (tooth) temperature to be 37°C and α = 1.7 × 10–5/°C, bulk modulus for copper = 140 × 109 N/m2.
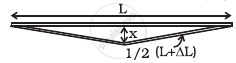
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
At what temperature a gold ring of diameter 6.230 cm be heated so that it can be fitted on a wooden bangle of diameter 6.241 cm? Both diameters have been measured at room temperature (27°C). (Given: coefficient of linear thermal expansion of gold αL = 1.4 × 10-5 K-1).
Each side of a box made of metal sheet in cubic shape is 'a' at room temperature 'T', the coefficient of linear expansion of the metal sheet is 'α'. The metal sheet is heated uniformly, by a small temperature ΔT, so that its new temeprature is T + ΔT. Calculate the increase in the volume of the metal box.
The height of mercury column measured with brass scale at temperature T0 is H0. What height H' will the mercury column have at T = 0°C. Coefficient of volume expansion of mercury is γ. Coefficient of linear expansion of brass is α ______.
Given below are two statements: one is labelled as Assertion A and the other is labelled as Reason R.
- Assertion A: When a rod lying freely is heated, no thermal stress is developed in it.
- Reason R: On heating, the length of the rod increases. In light of the above statements.
choose the correct answer from the options given below:
A solid metallic cube having a total surface area of 24 m2 is uniformly heated. If its temperature is increased by 10°C, calculate the increase in the volume of the cube.
(Given: α = 5.0 × 10-4°C-1)
A metal rod Y = 2 × 1012 dyne cm-2 of coefficient of linear expansion 1.6 × 10-5 per °C has its temperature raised by 20°C. The linear compressive stress to prevent the expansion of the rod is ______.
