Advertisements
Advertisements
Question
A glass flask has a volume 1 × 10−4 m3. It is filled with a liquid at 30°C. If the temperature of the system is raised to 100°C, how much of the liquid will overflow? (Coefficient of volume expansion of glass is 1.2 × 10−5 (°C)−1 while that of the liquid is 75 × 10−5 (°C)−1).
Solution
Given: V1 = 1 × 10−4 m3 = 10−4 m3, T1 = 30°C, T2 = 100°C, γglass = 1.2 × 10−5 , `γ_"liquid"` = 75 × 10−5
To find: Volume of liquid that overflows
Formula: `gamma = (V_2 - V_1)/(V_1(T_2 - T_1))`
Calculation: From formula,
Increase in volume = V2 − V1 = γ = V1(T2 − T1)
Increase in volume of glass
= γglass = V1(T2 − T1)
= 1.2 × 10−5 × 10−4 × (100 − 30)
= 1.2 × 70 × 10−9
= 8.4 × 10−8 m3
∴ Increase in volume of glass = 8.4 × 10−8 m3
Increase in volume of liquid -
= `γ_"liquid"`= V1(T2 − T1)
= 75 × 10−5 × 10-4 × (100 − 30)
= 75 × 70 × 10−9
= 5250 × 10−9 m3
∴ Increase in volume of liquid = 5250 × 10−9 m3
∴ Volume of liquid which overflows
= (5250 − 84) × 10−9 m3
= 5166 × 10−9 m3
= 0.5166 × 10−8 m3
∴ Volume of liquid that overflows is 0.5166 × 10−8 m3
APPEARS IN
RELATED QUESTIONS
A steel tape 1m long is correctly calibrated for a temperature of 27.0 °C. The length of a steel rod measured by this tape is found to be 63.0 cm on a hot day when the temperature is 45.0 °C. What is the actual length of the steel rod on that day? What is the length of the same steel rod on a day when the temperature is 27.0 °C? Coefficient of linear expansion of steel = 1.20 × 10–5 K–1
A hole is drilled in a copper sheet. The diameter of the hole is 4.24 cm at 27.0 °C. What is the change in the diameter of the hole when the sheet is heated to 227 °C? Coefficient of linear expansion of copper = 1.70 × 10–5 K–1.
A brass rod of length 50 cm and diameter 3.0 mm is joined to a steel rod of the same length and diameter. What is the change in length of the combined rod at 250 °C, if the original lengths are at 40.0 °C? Is there a ‘thermal stress’ developed at the junction? The ends of the rod are free to expand (Co-efficient of linear expansion of brass = 2.0 × 10–5 K–1, steel = 1.2 × 10–5 K–1).
A 10 kW drilling machine is used to drill a bore in a small aluminium block of mass 8.0 kg. How much is the rise in temperature of the block in 2.5 minutes, assuming 50% of power is used up in heating the machine itself or lost to the surroundings Specific heat of aluminium = 0.91 J g–1 K–1
If mercury and glass had equal coefficients of volume expansion, could we make a mercury thermometer in a glass tube?
Is it possible for two bodies to be in thermal equilibrium if they are not in contact?
A system X is neither in thermal equilibrium with Y nor with Z. The systems Y and Z
For a constant-volume gas thermometer, one should fill the gas at
Answer the following question.
Give an example of the disadvantages of thermal stress in practical use?
Solve the following problem.
In olden days, while laying the rails for trains, small gaps used to be left between the rail sections to allow for thermal expansion. Suppose the rails are laid at room temperature 27 °C. If maximum temperature in the region is 45 °C and the length of each rail section is 10 m, what should be the gap left given that α = 1.2 × 10–5K–1 for the material of the rail section?
A metre scale made of a metal reads accurately at 25 °C. Suppose in an experiment an accuracy of 0.12 mm in 1 m is required, the range of temperature in which the experiment can be performed with this metre scale is ______.(coefficient of linear expansion of the metal is `20 xx 10^-6 / (°"C")`
A metal sphere 10.01 cm in diameter is placed on a brass ring of internal diameter 10 cm and at the same temperature of 12° C. The temperature up to which they should be heated together so that the metal sphere just passes through the ring is `[alpha_"metal"= 12 xx 10^-6//°"C" and alpha_"brass" =18 xx 10^-6//°"C"]` ____________.
A metal rod is heated to t°C. A metal rod has length, area of cross-section, Young's modulus and coefficient of linear expansion as 'L', 'A', 'Y' and 'a' respectively. When the rod is heated, the work performed is ______.
A hot body at a temperature 'T' is kept in a surrounding of temperature 'T0'. It takes time 't1' to cool from 'T' to 'T2', time t2 to cool from 'T2' to 'T3' and time 't3' to cool from 'T3' to 'T4'. If (T - T2) = (T2 - T3) = (T3 - T4), then ______.
The volume of a metal block changes by 0.86% when heated through 200 °C then its coefficient of cubical expansion is ______.
As the temperature is increased, the time period of a pendulum ______.
A student records the initial length l, change in temperature ∆T and change in length ∆l of a rod as follows:
| S.No. | l(m) | ∆T (C) | ∆l (m) |
| 1. | 2 | 10 | `4 xx 10^-4` |
| 2. | 1 | 10 | `4 xx 10^-4` |
| 3. | 2 | 20 | `2 xx 10^-4` |
| 4. | 3 | 10 | `6 xx 10^-4` |
If the first observation is correct, what can you say about observations 2, 3 and 4.
Find out the increase in moment of inertia I of a uniform rod (coefficient of linear expansion α) about its perpendicular bisector when its temperature is slightly increased by ∆T.
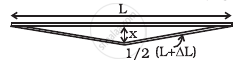
A rail track made of steel having length 10 m is clamped on a raillway line at its two ends (figure). On a summer day due to rise in temperature by 20° C, it is deformed as shown in figure. Find x (displacement of the centre) if αsteel = 1.2 × 10–5/°C.
At what temperature a gold ring of diameter 6.230 cm be heated so that it can be fitted on a wooden bangle of diameter 6.241 cm? Both diameters have been measured at room temperature (27°C). (Given: coefficient of linear thermal expansion of gold αL = 1.4 × 10-5 K-1).
The height of mercury column measured with brass scale at temperature T0 is H0. What height H' will the mercury column have at T = 0°C. Coefficient of volume expansion of mercury is γ. Coefficient of linear expansion of brass is α ______.
A disc is rotating freely about its axis. The percentage change in angular velocity of a disc if temperature decreases by 20°C is ______.
(coefficient of linear expansion of material of disc is 5 × 10-4/°C)
If the temperature of the sun were to increase from T to 2T and its radius from R to 2R, then the ratio of the radiant energy received on earth to what it was previously will be ______.
A glass flask is filled up to a mark with 50 cc of mercury at 18°C. If the flask and contents are heated to 38°C, how much mercury will be above the mark? (α for glass is 9 × 10-6/°C and coefficient of real expansion of mercury is 180 × 10-6/°C)
A clock with an iron pendulum keeps the correct time at 15°C. If the room temperature is 20°C, the error in seconds per day will be near ______.
(coefficient of linear expansion of iron is 1.2 × 10-5/°C)
A metal rod Y = 2 × 1012 dyne cm-2 of coefficient of linear expansion 1.6 × 10-5 per °C has its temperature raised by 20°C. The linear compressive stress to prevent the expansion of the rod is ______.
