Advertisements
Advertisements
Question
If points A(h, 0), B(0, k) and C(a, b) lie on a line then show that `"a"/"h" + "b"/"k"` = 1
Solution
A(h, 0), B(0, k) and C(a, b) lie on a line.
∴ A, B, C are collinear.
∴ slope of AB = slope of BC
∴ `("k" - 0)/(0 - "h") = ("b" - "k")/("a" - 0)`
∴ `- "k"/"h" = ("b" - "k")/"a"`
∴ – ak = bh – hk
∴ ak + bh = hk
∴ `("ak" + "bh")/"hk"` = 1
∴ `"a"/"h" + "b"/"k"` = 1
which is the required condition.
APPEARS IN
RELATED QUESTIONS
Find the slope of the following line which passes through the points:
C(−2, 3), D(5, 7)
Find the slope of the following line which passes through the points:
G(7, 1), H(−3, 1)
Find the slope of the line which makes angle of 45° with the positive direction of the Y-axis measured anticlockwise
Find the acute angle between the X-axis and the line joining points A(3, −1) and B(4, −2).
Select the correct option from the given alternatives:
If A is (5, −3) and B is a point on the x-axis such that the slope of line AB is −2 then B ≡
Answer the following question:
Find the value of k if the slope of the line passing through the points P(3, 4), Q(5, k) is 9
Answer the following question:
Find the value of k the points A(1, 3), B(4, 1), C(3, k) are collinear
Find the equation of the lines passing through the point (1, 1) with y-intercept (– 4)
Find the equation of the lines passing through the point (1,1) with slope 3
Find the equation of the lines passing through the point (1, 1) and the perpendicular from the origin makes an angle 60° with x-axis
If P(r, c) is midpoint of a line segment between the axes then show that `x/"r" + y/"c"` = 2
Find the equation of the line passing through the point (1, 5) and also divides the co-ordinate axes in the ratio 3:10
If p is length of perpendicular from origin to the line whose intercepts on the axes are a and b, then show that `1/("p"^3) = 1/("a"^2) + 1/("b"^2)`
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the linear relationship between C and F
The normal boiling point of water is 100°C or 212°F and the freezing point of water is 0°C or 32°F. Find the value of C for 98.6°F
Population of a city in the years 2005 and 2010 are 1,35,000 and 1,45,000 respectively. Find the approximate population in the year 2015. (assuming that the growth of population is constant)
Find the equation of the line, if the perpendicular drawn from the origin makes an angle 30° with x-axis and its length is 12
Show that the points (1, 3), (2, 1) and `(1/2, 4)` are collinear, by using a straight line
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross a pole
A 150 m long train is moving with constant velocity of 12.5 m/s. Find time taken to cross the bridge of length 850 m
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
Draw a graph showing the results.
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
What is the actual length of the spring
A spring was hung from a hook in the ceiling. A number of different weights were attached to the spring to make it stretch, and the total length of the spring was measured each time is shown in the following table
| Weight (kg) | 2 | 4 | 5 | 8 |
| Length (cm) | 3 | 4 | 4.5 | 6 |
How long will the spring be when 6 kilograms of weight on it?
A family is using Liquefied petroleum gas (LPG) of weight 14.2 kg for consumption. (Full weight 29.5kg includes the empty cylinders tare weight of 15.3kg.). If it is used with constant rate then it lasts for 24 days. Then the new cylinder is replaced. Draw the graph for first 96days
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the heights at which the escalator changes its direction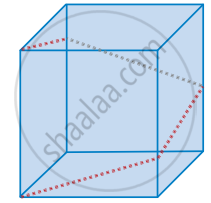
In a shopping mall there is a hall of cuboid shape with dimension 800 × 800 × 720 units, which needs to be added the facility of an escalator in the path as shown by the dotted line in the figure. Find the slopes of the escalator at the turning points
Choose the correct alternative:
Straight line joining the points (2, 3) and (−1, 4) passes through the point (α, β) if
Choose the correct alternative:
The y-intercept of the straight line passing through (1, 3) and perpendicular to 2x − 3y + 1 = 0 is
If one of the lines given by kx2 + 2xy – 3y2 = 0 is perpendicular to the line 3x + 5y+ 1 = 0, then the value of k is ______.
A point on the straight line, 3x + 5y = 15 which is equidistant from the coordinate, axes will lie only in ______.
The locus of the point of intersection of the lines xcosα + ysinα = α and xsinα – ycosα = b(where α is a variable) is ______.
The coordinates of vertices of base BC of an isosceles triangle ABC are given by B(1, 3) and C(–2, 7) which of the following points can be the possible coordinates of the vertex A?
The locus of the midpoint of the portion intercept between the axes by the line xcosa + ysina = P where P is a constant is ______.
Find the coordinates of the point which divides the line segment joining the points (1, –2, 3) and (3, 4, –5) internally in the ratio 2 : 3.
The equation of the line passing through the point (–3, 1) and bisecting the angle between co-ordinate axes is ______.
If planes x – cy – bz = 0, cx – y + az = 0 and bx + ay – z = 0 pass through a straight line then a2 + b2 + c2 = ______.
Find the transformed equation of the straight line 2x – 3y + 5 = 0, when the origin is shifted to the point (3, –1) after translation of axes.
