Advertisements
Advertisements
Question
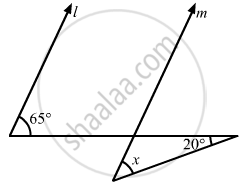
In the given figure, if lines l and m are parallel, then x =
Options
20°
45°
65°
85°
Solution
The given figure is as follows:
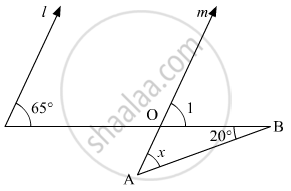
Since, l || m. Thus, 65° angle and ∠1 are corresponding angles.
Therefore,
∠1= 65° (i)
In a triangle, we know that, the exterior angle is equal to the sum of the interior opposite angle.
In ΔAOB:
∠1 = x +20°
x = ∠1 - 20°
From equation (i):
x = 65° - 20°
x = 45°
APPEARS IN
RELATED QUESTIONS
If two straight lines are perpendicular to the same line, prove that they are parallel to each
other.
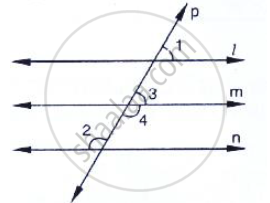
In the below fig, if l || m || n and `∠`1 = 60°, find `∠`2.
Prove that the straight lines perpendicular to the same straight line are parallel to one
another.
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then alternate interior angles are equal.
Which of the following statement are true and false ? Give reason.
If two parallel lines are intersected by a transversal, then the interior angles on the same side of the transversal are equal.
Fill in the blank in the following to make the statement true:
If a transversal intersects a pair of lines in such a way that a pair of alternate angles
are equal, then the lines are _______
In the given figure, if l1 || l2 and l3 || l4, what is y in terms of x?

AB and CD are two parallel lines. PQ cuts AB and CD at E and F respectively. EL is the bisector of ∠FEB. If ∠LEB = 35°, then ∠CFQ will be
In the given figure, If line segment AB is parallel to the line segment CD, what is the value of y?

In the following figure, bisectors AP and BQ of the alternate interior angles are parallel, then show that l ||m.