Advertisements
Advertisements
Question
In ∆PQR, PQ = √8 , QR = √5 , PR = √3. Is ∆PQR a right-angled triangle? If yes, which angle is of 90°?
Advertisements
Solution
In ∆PQR, PQ = √8 , QR = √5 , PR = √3
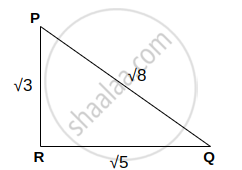
Longest side of ∆PQR = PQ = √8
∴ PQ2 = (√8)2 = 8
Now, the sum of the squares of the remaining sides is
QR2 + PR2 = (√5)2 + (√3)2 = 5 + 3 = 8
∴ PQ2 = QR2 + PR2
∴ The square of the longest side is equal to the sum of the squares of the remaining two sides.
by Converse of Pythagoras theorem,
∴ ∆PQR is a right-angled triangle.
Now, PQ is the hypotenuse.
∴ ∠PRQ = 90° ...(Angle opposite to hypotenuse)
∴ ∆PQR is a right-angled triangle in which ∠PRQ is 90°.
APPEARS IN
RELATED QUESTIONS
Sides of the triangle are 7 cm, 24 cm, and 25 cm. Determine whether the triangle is a right-angled triangle or not.
In the rectangle WXYZ, XY + YZ = 17 cm, and XZ + YW = 26 cm. Calculate the length and breadth of the rectangle?
In the adjacent figure, ABC is a right angled triangle with right angle at B and points D, E trisect BC. Prove that 8AE2 = 3AC2 + 5AD2
In a ∆ABC, AD is the bisector of ∠BAC. If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
8, 15, 17
Check whether given sides are the sides of right-angled triangles, using Pythagoras theorem
12, 13, 15
Choose the correct alternative:
In right angled triangle, if sum of the squares of the sides of right angle is 169, then what is the length of the hypotenuse?
Choose the correct alternative:
A rectangle having length of a side is 12 and length of diagonal is 20, then what is length of other side?
Choose the correct alternative:
If length of both diagonals of rhombus are 60 and 80, then what is the length of side?
A rectangle having dimensions 35 m × 12 m, then what is the length of its diagonal?
In ∆LMN, l = 5, m = 13, n = 12 then complete the activity to show that whether the given triangle is right angled triangle or not.
*(l, m, n are opposite sides of ∠L, ∠M, ∠N respectively)
Activity: In ∆LMN, l = 5, m = 13, n = `square`
∴ l2 = `square`, m2 = 169, n2 = 144.
∴ l2 + n2 = 25 + 144 = `square`
∴ `square` + l2 = m2
∴By Converse of Pythagoras theorem, ∆LMN is right angled triangle.
In ΔABC, AB = 9 cm, BC = 40 cm, AC = 41 cm. State whether ΔABC is a right-angled triangle or not. Write reason.
In the given figure, triangle PQR is right-angled at Q. S is the mid-point of side QR. Prove that QR2 = 4(PS2 – PQ2).
