Advertisements
Advertisements
Question
In ∆RST, ∠S = 90°, ∠T = 30°, RT = 12 cm then find RS and ST.
Solution
In ∆RST,
∠S = 90∘, ∠T = 30∘, ∴ ∠R = 60∘
By 30∘ − 60∘ − 90∘ theorem,
\[ \Rightarrow RS = \frac{1}{2} \times 12\]
\[ \Rightarrow RS = 6 cm . . . \left( 1 \right)\]
\[ST = \frac{\sqrt{3}}{2} \times RT\]
\[ \Rightarrow ST = \frac{\sqrt{3}}{2} \times 12\]
\[ \Rightarrow ST = 6\sqrt{3} cm . . . \left( 2 \right)\]
Hence, RS = 6 cm and ST = 6\[\sqrt{3}\] cm.
APPEARS IN
RELATED QUESTIONS
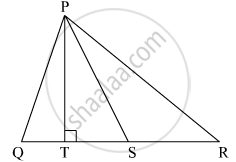
In the given figure, seg PS is the median of ∆PQR and PT ⊥ QR. Prove that,
PR2 = PS2 + QR × ST + `("QR"/2)^2`
Some question and their alternative answer are given. Select the correct alternative.
In ∆ABC, AB = \[6\sqrt{3}\] cm, AC = 12 cm, BC = 6 cm. Find measure of ∠A.
Do sides 7 cm, 24 cm, 25 cm form a right angled triangle ? Give reason
Find the length a diagonal of a rectangle having sides 11 cm and 60 cm.
A side of an isosceles right angled triangle is x. Find its hypotenuse.
In ∆ABC, seg AP is a median. If BC = 18, AB2 + AC2 = 260, Find AP.
Sum of the squares of adjacent sides of a parallelogram is 130 sq.cm and length of one of its diagonals is 14 cm. Find the length of the other diagonal.
Seg PM is a median of ∆PQR. If PQ = 40, PR = 42 and PM = 29, find QR.
Seg AM is a median of ∆ABC. If AB = 22, AC = 34, BC = 24, find AM
Choose the correct alternative:
Out of the following which is a Pythagorean triplet?
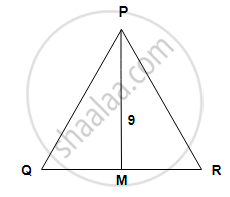
In ΔPQR, seg PM is a median, PM = 9 and PQ2 + PR2 = 290. Find the length of QR.
In ΔPQR, seg PM is the median. If PM = 9, PQ2 + PR2 = 290, Find QR.
Height and base of a right angled triangle are 24 cm and 18 cm. Find the length of its hypotenus?
"The diagonals bisect each other at right angles." In which of the following quadrilaterals is the given property observed?
Which of the following figure is formed by joining the mid-points of the adjacent sides of a square?
In the given figure, triangle ABC is a right-angled at B. D is the mid-point of side BC. Prove that AC2 = 4AD2 – 3AB2.

