Advertisements
Advertisements
Questions
Income of 100 students of their parents is given as follows:
| Income (in thousand Rs.) |
No. of students (f) |
| 0 – 8 | 8 |
| 8 – 16 | 35 |
| 16 – 24 | 35 |
| 24 – 32 | 14 |
| 32 – 40 | 8 |
Draw an ogive for the given distribution on a graph sheet. Use a suitable scale for your exercise. Use your ogive to estimate:
- the median income.
- Calculate the income below which freeship will be awarded to students if their parents income is in the bottom 15%
- Mean income.
The incomes of the parents of 100 students in a class in a certain university are tabulated below.
| Income (in thousand ₹) |
0 – 8 | 8 – 16 | 16 – 24 | 24 – 32 | 32 – 40 |
| No. of students | 8 | 35 | 35 | 14 | 8 |
- Draw a cumulative frequency curve to estimate the median income.
- If 15% of the students are given freeships on the basis of the income of their parents, find the annual income of parents, below which the freeships will be awarded.
- Calculate the Arithmetic mean.
Solution
i. Cumulative frequency curve
| Income (in thousand Rs.) |
No. of students (f) |
Cumulative Frequency |
Class Mark x |
fx |
| 0 – 8 | 8 | 8 | 4 | 32 |
| 8 – 16 | 35 | 43 | 12 | 420 |
| 16 – 24 | 35 | 78 | 20 | 700 |
| 24 – 32 | 14 | 92 | 28 | 392 |
| 32 – 40 | 8 | 100 | 36 | 288 |
| `sumf = 100` | `sumfx = 1832` |
We plot the points (8, 8), (16, 43), (24, 78), (32, 92) and (40, 100) to get the curve as follows:
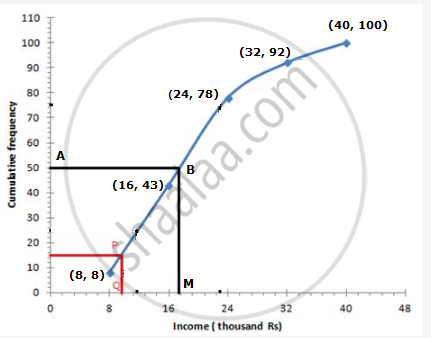
Here, N = 100
`=> N/2 = 50`
At y = 50, affix A.
Through A, draw a horizontal line meeting the curve at B.
Through B, a vertical line is drawn which meets OX at M.
OM = 17.6 units
Hence, median income = 17.6 thousands
ii. 15% of 100 student = `(15 xx 100)/100 = 15`
From c.f. 15, draw a horizontal line which intersects the curve at P.
From P, draw a perpendicular to x-axis meeting it at Q which is equal to 9.6.
Therefore, freeship will be awarded to students provided annual income of their parents is upto 9.6 thousands.
iii. Mean = `(sumfx)/(sumf) = 1832/100 = 18.32`
APPEARS IN
RELATED QUESTIONS
The marks obtained by 120 students in a test are given below:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of students |
5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Draw an ogive for the given distribution on a graph sheet.
Use a suitable scale for ogive to estimate the following:
(1) The median.
(2) The number of students who obtained more than 75% marks in the test.
(3) The number of students who did not pass the test if minimum marks required to pass is 40
Marks obtained by 200 students in an examination are given below:
| Marks | No. of students |
| 0 – 10 | 5 |
| 10 – 20 | 11 |
| 20 – 30 | 10 |
| 30 – 40 | 20 |
| 40 – 50 | 28 |
| 50 – 60 | 37 |
| 60 – 70 | 40 |
| 70 – 80 | 29 |
| 80 – 90 | 14 |
| 90 – 100 | 6 |
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine:
- The median marks.
- The number of students who failed if minimum marks required to pass is 40.
- If scoring 85 and more marks are considered as grade one, find the number of students who secured grade one in the examination.
- Use the information given in the adjoining histogram to construct a frequency table.
- Use this table to construct an ogive.
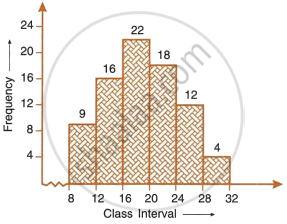
| Class mark | 12.5 | 17.5 | 22.5 | 27.5 | 32.5 | 37.5 | 42.5 |
| Frequency | 12 | 17 | 22 | 27 | 30 | 21 | 16 |
- From the distribution, given above, construct a frequency table.
- Use the table obtained in part (a) to draw : (i) a histogram, (ii) an ogive.
Marks obtained by 200 students in an examination are given below:
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80 - 90 | 90 - 100 |
| Frequency | 5 | 11 | 10 | 20 | 28 | 37 | 40 | 29 | 14 | 6 |
Draw an ogive for the given distribution taking 2 cm = 10 marks on one axis and 2 cm = 20 students on the other axis. Using the graph, determine:
(i) The median marks
(ii) The number of students who failed if minimum marks required to pass is 40.
(iii) If scoring 85 and more marks is considered as grade one, find the number of students who secured grade one in the examination.
Attempt this question on graph paper. Marks obtained by 200 students in examination are given below:
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80 - 90 | 90 - 100 |
| No. of students | 5 | 10 | 14 | 21 | 25 | 34 | 36 | 27 | 16 | 12 |
Draw an ogive for the given distribution taking 2 cm = 10 makrs on one axis and 2 cm = 20 students on the other axis.
From the graph find:
(i) the median
(ii) the upper quartile
(iii) number of student scoring above 65 marks.
(iv) If to students qualify for merit scholarship, find the minimum marks required to qualify.
The mark of 200 students in a test were recorded as follows:
| Marks % | No. of students |
| 10 - 19 | 7 |
| 20 - 29 | 11 |
| 30 - 39 | 20 |
| 40 - 49 | 46 |
| 50 - 59 | 57 |
| 60 - 69 | 37 |
| 70 - 79 | 15 |
| 80 - 89 | 7 |
Draw the cumulative frequency table.
Draw an ogive and use it to find:
(i) The median
(ii) The number of students who scored more than 35% marks.
Use graph paper for this question.
The table given below shows the monthly wages of some factory workers.
(i) Using the table, calculate the cumulative frequency of workers.
(ii) Draw the cumulative frequency curve.
Use 2 cm = ₹500, starting the origin at ₹6,500 on X-axis, and 2 cm = 100 worker at they Y-axis.
(iii) Use your graph to write down the median wages in ₹.
| Wages in ₹ (CLass) |
No. of workers (frequency) | Cumulative frequency f(x) |
| 6500 - 7000 | 10 | - |
| 7000 - 7500 | 18 | - |
| 7500 - 8000 | 22 | - |
| 8000 - 8500 | 25 | - |
| 8500 - 9000 | 17 | - |
| 9000 - 9500 | 10 | - |
| 9500 - 10000 | 8 | - |
The marks obtained by 120 students in a test are given below:
| Marks | 0 - 10 | 10 - 20 | 20 - 30 | 30 - 40 | 40 - 50 | 50 - 60 | 60 - 70 | 70 - 80 | 80 - 90 | 90 - 100 |
| No. of Students | 5 | 9 | 16 | 22 | 26 | 18 | 11 | 6 | 4 | 3 |
Draw an ogive for the given distribution on a graph sheet.
Use suitable scale for ogive to estimate the following :
(i) the median.
(ii) The number of students who obtained more than 75% marks in the test.
The marks obtained by 100 students in a Mathematics test are given below:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
| No. of Students | 3 | 7 | 12 | 17 | 23 | 14 | 9 | 6 | 5 | 4 |
Draw an ogive for the given distribution on a graph sheet.
Use a scale of 2 cm = 10 units on both axes.
Use the ogive to estimate the :
- median.
- lower quartile.
- number of students who obtained more than 85% marks in the test.
- number of students who did not pass in the test if the pass percentage was 35.
