Advertisements
Advertisements
Question
The marks of 20 students in a test were as follows:
2, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19 and 20.
Calculate:
- the mean
- the median
- the mode
Solution
Arranging the terms in ascending order:
2, 6, 8, 9, 10, 11, 11, 12, 13, 13, 14, 14, 15, 15, 15, 16, 16, 18, 19, 20
Number of terms = 20
Σx = 2 + 6 + 8 + 9 + 10 + 11 + 11 + 12 + 13 + 13 + 14 + 14 + 15 + 15 + 15 + 16 + 16 + 18 + 19 + 20 = 257
i. Mean = `(∑x)/(∑n) = 257/20 = 12.85`
ii. Median = `(10^(th) term + 11^(th) term)/2`
= `(13 + 14)/2`
= `27/2`
= 13.5
iii. Mode = 15 as it has maximum frequencies i.e. 3
APPEARS IN
RELATED QUESTIONS
Using the information given in the adjoining histogram, calculate the mean.
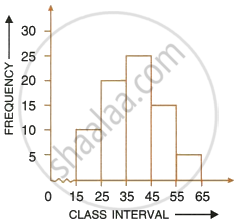
At a shooting competition the score of a competitor were as given below:
| Score | 0 | 1 | 2 | 3 | 4 | 5 |
| No. of shots | 0 | 3 | 6 | 4 | 7 | 5 |
- What was his modal score?
- What was his median score?
- What was his total score?
- What was his mean score?
The marks obtained by 120 students in a mathematics test is given below:
| Marks | No. of students |
| 0 – 10 | 5 |
| 10 – 20 | 9 |
| 20 – 30 | 16 |
| 30 – 40 | 22 |
| 40 – 50 | 26 |
| 50 – 60 | 18 |
| 60 – 70 | 11 |
| 70 – 80 | 6 |
| 80 – 90 | 4 |
| 90 – 100 | 3 |
Draw an ogive for the given distributions on a graph sheet. Use a suitable scale for your ogive. Use your ogive to estimate:
- the median
- the number of student who obtained more than 75% in test.
- the number of students who did not pass in the test if the pass percentage was 40.
- the lower quartile.
Find the mean of the following frequency distribution :
| class | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
| Frequency | 7 | 5 | 10 | 12 | 6 |
Find the mode of the following frequency distribution:
| Hrs. Spent daily in studies | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 |
| No. of students | 8 | 7 | 3 | 5 | 10 | 6 | 3 | 4 |
Draw a histogram for the following distribution and estimate the mode:
| I.Q. Score | 80-100 | 100-120 | 120-140 | 140-160 | 160-180 | 180-200 |
| No. of Students | 6 | 9 | 16 | 13 | 4 | 2 |
Find the mean of first ten odd natural numbers.
Find the mean of: 12, 9, 6,11 and 17
Median is one of the observations in the data if number of observations is ______.
The measures of central tendency may not lie between the maximum and minimum values of data.
